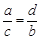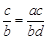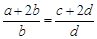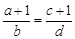题目内容
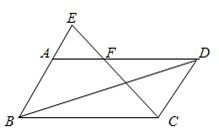
如图，已知AB∥EF∥CD，AD与BC相交于点O．
（1）如果CE=3，EB=9，DF=2，求AD的长；
（2）如果BO：OE：EC=2：4：3，AB=3，求CD的长．
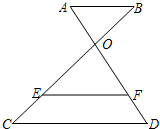
（1）如果CE=3，EB=9，DF=2，求AD的长；
（2）如果BO：OE：EC=2：4：3，AB=3，求CD的长．
（1）∵CE=3，EB=9，
∴BC=CE+EB=12．
∵AB∥EF，
∴
=
，则
=
．
又EF∥CD，
∴
=
，则
=
，
∴
=
，即
=
，
∴AF=6，
∴AD=AF+FD=6+2=8，即AD的长是8；
（2）∵AB∥CD，
∴BO：OE=AB：EF．
又BO：OE=2：4，AB=3，
∴EF=6．
∵EF∥CD，
∴
=
．
又∵OE：EC=4：3，
∴
=
，
∴
=
，
∴CD=
EF=10.5，即CD的长是10.5．
∴BC=CE+EB=12．
∵AB∥EF，
∴
| FO |
| AF |
| EO |
| EB |
| FO |
| EO |
| AF |
| EB |
又EF∥CD，
∴
| FO |
| FD |
| EO |
| EC |
| FO |
| EO |
| FD |
| EC |
∴
| AF |
| EB |
| FD |
| EC |
| AF |
| 9 |
| 2 |
| 3 |
∴AF=6，
∴AD=AF+FD=6+2=8，即AD的长是8；
（2）∵AB∥CD，
∴BO：OE=AB：EF．
又BO：OE=2：4，AB=3，
∴EF=6．
∵EF∥CD，
∴
| OE |
| OC |
| EF |
| CD |
又∵OE：EC=4：3，
∴
| OE |
| OC |
| 4 |
| 7 |
∴
| EF |
| CD |
| 4 |
| 7 |
∴CD=
| 7 |
| 4 |
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
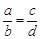，那么下列各式中一定成立的是（ ）
