Question

已知：如图所示，点D、E在△ABC的边BC上，AB＝AC，AD＝AE．

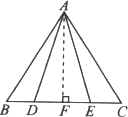
求证：BD＝CE．

Answer 1

答案：
解析：

解答：作AF⊥BC，垂足为F，则AF⊥DE， 　　∵在△ABC中，AB＝AC，AF⊥BC，∴BF＝CF， 　　又∵在△ADE中，AD＝AE，AF⊥DE，∴DF＝EF， 　　∴BF－DF＝CF－EF，即BD＝CE． 　　评析：在等腰三角形中，虽然顶角的平分线、底边上的高、中线互相重合，但作辅助线时，要视具体情况而定，不能随意作其中一条，否则证明变得复杂，甚至很难证明．

提示：

因为△ABC和△ADE都是等腰三角形，故可作底边上的高AF，利用“三线合一”转化为中线易得BD＝CE．