题目内容
(2011•成华区二模)某校九年级各班分别选出3名学生组成班级代表队,参加以“城市,让生活更美好(Better City,Bett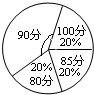 er Life)”为主题的世博知识竞赛,竞赛规定得分最多的班级为优胜班级.各代表队比赛结果如下:
er Life)”为主题的世博知识竞赛,竞赛规定得分最多的班级为优胜班级.各代表队比赛结果如下:
(1)写出表格中得分的众数,中位数和平均数;
(2)若将各班级代表队的得分情况绘制成右图所示的扇形统计图,则得分为90分所占扇形的圆心角是多少?
(3)学校决定从获胜班级的代表队中各抽取1名学生与一位教师组成“上海世博宣传小组”.已知李浩、赵华分别是获胜班级代表队的1名学生,请用列表法或画树状图的方法求“上海世博宣传小组”中至少有他们俩位中的一位的概率P.(注:获胜班级代表队的其他学生可用不同字母表示)
 er Life)”为主题的世博知识竞赛,竞赛规定得分最多的班级为优胜班级.各代表队比赛结果如下:
er Life)”为主题的世博知识竞赛,竞赛规定得分最多的班级为优胜班级.各代表队比赛结果如下:| 班级 | 九(1) | 九(2) | 九(3) | 九(4) | 九(5) | 九(6) | 九(7) | 九(8) | 九(9) | 九(10) |
| 得分 | 85 | 90 | 100 | 90 | 80 | 80 | 90 | 100 | 85 | 90 |
(2)若将各班级代表队的得分情况绘制成右图所示的扇形统计图,则得分为90分所占扇形的圆心角是多少?
(3)学校决定从获胜班级的代表队中各抽取1名学生与一位教师组成“上海世博宣传小组”.已知李浩、赵华分别是获胜班级代表队的1名学生,请用列表法或画树状图的方法求“上海世博宣传小组”中至少有他们俩位中的一位的概率P.(注:获胜班级代表队的其他学生可用不同字母表示)
分析:(1)根据众数,中位数和平均数定义求解即可求得答案;
(2)首先求得得分为90分所占的百分比,再乘以360°,即可求得得分为90分所占扇形的圆心角是多少;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与“上海世博宣传小组”中至少有他们俩位中的一位的情况,再利用概率公式求解即可求得答案.
(2)首先求得得分为90分所占的百分比,再乘以360°,即可求得得分为90分所占扇形的圆心角是多少;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与“上海世博宣传小组”中至少有他们俩位中的一位的情况,再利用概率公式求解即可求得答案.
解答:解:(1)众数为90,中位数为90,平均数为:
=89;
(2)∵1-20%-20%-20%=40%,
∴40%×360°=144°,
∴得分为90分所占扇形的圆心角是144°;
(3)根据题意得:获胜班级代表队为九(3)与九(8),
将九(3)的另两位同学用A与B表示,九(8)的另两位同学用C与D表示,
画树状图得:
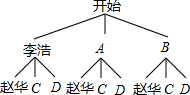
∵共有9种等可能的结果,“上海世博宣传小组”中至少有他们俩位中的一位的有5种情况,
∴“上海世博宣传小组”中至少有他们俩位中的一位的概率为:
.
| 80×2+85×2+90×4+100×2 |
| 10 |
(2)∵1-20%-20%-20%=40%,
∴40%×360°=144°,
∴得分为90分所占扇形的圆心角是144°;
(3)根据题意得:获胜班级代表队为九(3)与九(8),
将九(3)的另两位同学用A与B表示,九(8)的另两位同学用C与D表示,
画树状图得:

∵共有9种等可能的结果,“上海世博宣传小组”中至少有他们俩位中的一位的有5种情况,
∴“上海世博宣传小组”中至少有他们俩位中的一位的概率为:
| 5 |
| 9 |
点评:此题考查的是用列表法或树状图法求概率,众数、中位数、平均数的知识以及扇形统计图.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011•成华区二模)小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上(如图),已知∠2=35°,则∠1的度数为( )
(2011•成华区二模)小明课间把老师的三角板的直角顶点放在黑板的两条平行线a、b上(如图),已知∠2=35°,则∠1的度数为( ) (2011•成华区二模)如图,已知点A是双曲线
(2011•成华区二模)如图,已知点A是双曲线 (2011•成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )
(2011•成华区二模)如图,在Rt△ABC中,∠ACB=30°,CD=4,BD平分∠ABC,交AC于点D,则点D到BC的距离是( )