题目内容
(本小题满分7分)如图,已知抛物线y1=-x2+bx+c经过A(1,0),B(0,-2)两点,顶点为D.
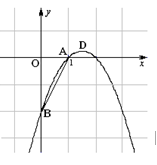
【小题1】(1)求抛物线y1 的解析式;
【小题2】(2)将△AOB绕点A逆时针旋转90°后,得到△AO′ B′ ,将抛物线y1沿对称轴平移后经过点B′ ,写出平移后所得的抛物线y2 的解析式;
【小题3】(3)设(2)的抛物线y2与
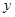 轴的交点为B1,顶点为D1,若点M在抛物线y2上,且满足△MBB1的面积是△MDD1面积的2倍,求点M的坐标.
轴的交点为B1,顶点为D1,若点M在抛物线y2上,且满足△MBB1的面积是△MDD1面积的2倍,求点M的坐标.

【小题1】解:(1)已知抛物线y1=-x2+bx+c经过点A(1,0), B(0,-2),
∴
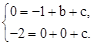 解得
解得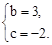
∴所求抛物线的解析式为y1=-x2 +3x-2
【小题2】(2)解法1:∵ A(1,0),B(0,-2), ∴ OA=1,OB=2.
由旋转性质可得O′A=OA=1,O′B′=OB=2.
∴ B′ 点的坐标为(3,-1) .
∵ 抛物线y1的顶点D (
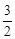 ,
,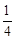 ),且抛物线y2 是由y1沿对称轴平移后得到的,
),且抛物线y2 是由y1沿对称轴平移后得到的,∴ 可设y2 的解析式为y2=" -" (x -
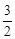 )2 +k .
)2 +k .∵ y2经过点B′,∴ - (3 -
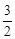 )2 +k= -1.解得k=
)2 +k= -1.解得k=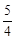 .
.∴ y2=" -" (x -
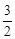 )2 +
)2 +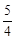 .…………………………………………………………… 4′
.…………………………………………………………… 4′解法2:同解法1 得B′ 点的坐标为 (3,-1) .
∵ 当x=3时,由y1=-x2 +3x-2得y=-2,可知抛物线y1过点(3,-2) .
∴ 将抛物线y1沿y轴向上平移1个单位后过点B′.
∴ 平移后的抛物线y2的解析式为:y2=-x2 +3x-1
【小题3】(3)∵ y1=-x2+3x-2 = -(x-
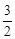 )2 +
)2 +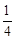 ,y2=-x2 +3x-1= -(x-
,y2=-x2 +3x-1= -(x-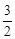 )2 +
)2 +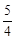 ,
,∴ 顶点D(
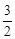 ,
,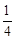 ),D1(
),D1(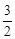 ,
,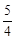 ).∴ DD1=1.
).∴ DD1=1.又B1(0,-2),B1(0,-1),∴BB1=1.
设M点坐标为(m,n) ,
∵ BB1=DD1,由
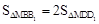 ,
,可知当m≤0时,符合条件的M点不存在;…………………………………… 5′
而当0<m<
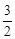 时,有m=2(
时,有m=2(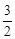 -m),解得m=1;
-m),解得m=1;当m>
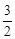 时,有m="2(m" -
时,有m="2(m" -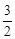 ),解得m=3.
),解得m=3.当m=1时,n=1;当m=3时,n=-1.
∴M1(1,1),M2(3,-1).解析:
略

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目




 不小于3cm吗?请说明理由.
不小于3cm吗?请说明理由. 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的 ,另一根露出水面的长度是它的
,另一根露出水面的长度是它的 .两根铁棒长度之和为55 cm.
.两根铁棒长度之和为55 cm.
 甲:
甲: 乙:
乙: =55
=55