Question

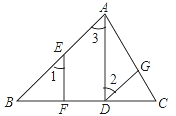
【题目】如图所示，已知AD，AE分别是△ADC和△ABC的高和中线，AB=6cm，AC=8cm，BC=10cm，∠CAB=90°．试求：

（1）AD的长；

（2）△ABE的面积；

（3）△ACE和△ABE的周长的差．

Answer 1

【答案】⑴24/5cm（4.8cm）；⑵12cm；⑶2cm.

【解析】

（1）利用直角三角形面积的两种求法求线段AD的长度即可；（2）先求△ABC的面积，再根据△AEC与△ABE是等底同高的两个三角形，它们的面积相等，由此即可求得△ABE的面；（3）由AE是中线，可得BE=CE，根据△ACE的周长-△ABE的周长=AC+AE+CE-（AB+BE+AE），化简可得△ACE的周长-△ABE的周长=AC-AB，即可求解．

∵∠BAC=90°，AD是边BC上的高，

∴ABAC=BCAD，

∴AD= =4.8（cm），

即AD的长度为4.8cm；

（2）如图，∵△ABC是直角三角形，∠BAC=90°，AB=6cm，AC=8cm，

∴S△ABC=ABAC=×6×8=24（cm2）．

又∵AE是边BC的中线，

∴BE=EC，

∴BEAD=ECAD，即S△ABE=S△AEC，

∴S△ABE=S△ABC=12（cm2）．

∴△ABE的面积是12cm2．

（3）∵AE为BC边上的中线，

∴BE=CE，

∴△ACE的周长-△ABE的周长=AC+AE+CE-（AB+BE+AE）=AC-AB=8-6=2（cm），

即△ACE和△ABE的周长的差是2cm．