题目内容
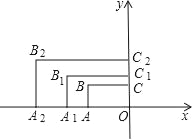
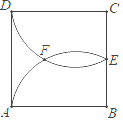
【题目】如图，正方形ABCD的边长为3a，两动点E，F分别从顶点B，C同时开始以相同速度沿边BC，CD运动，与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF，对应边EG＝BC，B，E，C，G在一条直线上.
（1）若BE＝a，求DH的长；
（2）当E点在BC边上的什么位置时，△DHE的面积取得最小值？并求该三角形面积的最小值.
【答案】（1）
a；（2）E为BC的中点时，
a2
【解析】
（1）可通过构建直角三角形求解．连接FH，则FH∥BE且FH=BE，FH⊥CD．因此三角形DFH为直角三角形．
点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动，那么DF=3a-a=2a，DF=2a，FH=a，根据勾股定理就求出了DH的长．
（2）设BE=x，△DHE的面积为y，通过三角形DHE的面积=三角形CDE的面积+梯形CDHG的面积-三角形EGH的面积，来得出关于x，y的函数关系式，然后根据函数的性质求出y取最小值时x的值，并求出此时y的值．
解：（1）连接FH，
∵△EGH≌△BCF，
∴HG＝FC，∠G＝∠BCF，
∴HG∥FC，
∴四边开FCGH是平行四边形，
∴FH∥CG，且FH＝CG，
又∵EG＝BC，
∴EG－EC＝BC－EC，即CG＝BE，
∴FH＝BE，
∵FH∥CG，
∴∠DFH＝∠DCG＝90°，
由题意可知：CF＝BE＝a，
在Rt△DFH中，DF＝3a－a＝2a，FH＝a，
∴DH＝
＝a；
（2）设BE＝x，△DHE的面积为y，根据题意得：
y＝S△CDE+S梯形CDHG－S△EGH＝
×3a(3a－x)+ (3a+x)x－×3a×x，
∴y＝x2－
ax+
a2＝(x－a)2+a2，
∴当x＝a，即E为BC的中点时，y取得最小值，即△DHE的面积取得最小值，最小值是a2.
