Question

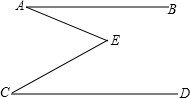
如图，直线AB∥CD，直线AB、CD被直线EF所截，EG平分∠BEF，FG平分∠DFE，求证：EG⊥FG．

Answer 1

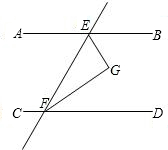
证明：∵AB∥CD，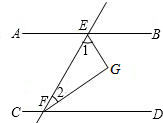
∴∠BEF+∠EFD=180°，
∵EG平分∠BEF，FG平分∠DFE，
∴∠1=

1

2

∠BEF，∠2=

1

2

∠EFD，
∴∠1+∠2=

1

2

（∠BEF+∠EFD）=

1

2

×180°=90°，
在△EFG中，
∠G=180°-∠1-∠2=90°，
∴EG⊥FG．