题目内容
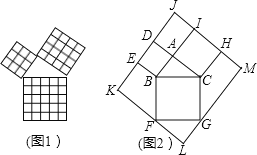
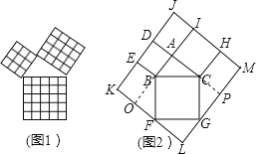
【题目】勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，已知∠BAC=90°，AB=6，AC=8，点D、E、F、G、H、I都在矩形KLMJ的边上，则矩形KLMJ的周长为（ ）
A. 40B. 44C. 84D. 88
【答案】C
【解析】
延长AB交KF于点O，延长AC交GM于点P，可得四边形AOLP是正方形，然后求出正方形的边长，再求出矩形KLMJ的长与宽，然后根据矩形的周长公式列式计算即可得解．
如图，延长AB交KF于点O，延长AC交GM于点P，
可证得四边形AOLP是正方形，边长AO=AB+AC=6+8=14，
∴KL=6+14=20，LM=8+14=22，
∴矩形KLMJ的周长为2×（20+22）=84．
故选:C．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
