��Ŀ����
����Ŀ�����Ķ����в��ϣ��������Ӧ������
�������Բ���������˽�Բ����������2000����ǰ�����ҹ���ī�Ӹ���Բ�ĸ����һ��ͬ��Ҳ��������˼˵��Բ��һ��Բ�ģ�Բ�ĵ�Բ�ܵij�����ȣ���������ϣ����ѧ��ŷ����ø�Բ�µĶ���Ҫ��100�꣮��Բ�йصĶ����кܶ࣬���нǶ�����������֮һ��
���ǰѶ�����Բ�ϣ�һ�ߺ�Բ�ཻ����һ�ߺ�Բ���еĽǽ������нǣ�
���нǶ��������нǵĶ������������л����Ե�Բ�ܽǶ�����
���������нǶ����IJ���֤�����̣�
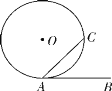
֤������ͼ�٣�AB���O�����ڵ�A����Բ��O����AC��ʱ�����õ���CAB��90�㣬�������нǡ�BAC�Ķ������������а�Բ���Ե�Բ�ܽǶ�����
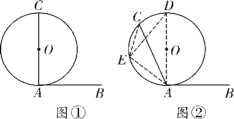
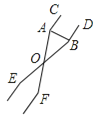
��ͼ�ڣ�AB���O�����ڵ�A����Բ��O�ڡ�BAC���ڲ�ʱ������A��ֱ��AD����O�ڵ�D����![]() ����ȡһ��E������EC��ED��EA�����CED����CAD��
����ȡһ��E������EC��ED��EA�����CED����CAD��
��
����
(1)�밴�������֤��˼·��д����֤����ʣ�ಿ�֣�
(2)��ͼ�ۣ�AB���O�����ڵ�A����Բ��O�ڡ�BAC���ⲿʱ����д�����нǶ�����֤�����̣�
���𰸡���1�������������2���������
��������
��1������Բ�ܽǶ����õ���DEA��90�����ٸ���ͬ�����Ե�Բ�ܽ���ȵõ���CED����CAD��������õ�ʽ�����ʼ��ɵõ���CEA����CAB��
��2��ͨ����C=90��˵����CFA����FAC��90�����ٸ���ͬ�ǵ������ȵõ���CAB����CFA����.
�⣺��1����AD�ǡ�Oֱ����
���DEA��90����
��AB���O�����ڵ�A��
���DAB��90����
���CED����DEA����CAD����DAB������CEA����CAB��
�����нǵĶ������������л����Ե�Բ�ܽǶ�����
��2��֤������ͼ������A��ֱ��AF����O�ڵ�F������FC��
��AF��ֱ����
���ACF��90����
���CFA����FAC��90����
��AB���O�����ڵ�A��
���FAB��90����
���CAB����FAC��90����
���CAB����CFA��
�����нǵĶ������������л����Ե�Բ�ܽǶ�����

 ��У����ϵ�д�
��У����ϵ�д�