题目内容
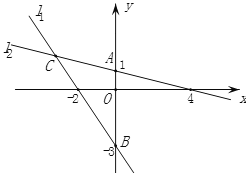
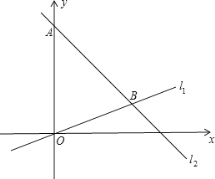
【题目】已知，如图，在平面直角坐标系内，点A的坐标为（0，24 ），经过原点的直线l1与经过点A的直线l2相交于点B，点B坐标为（18，6）.
(1)求直线l1，l2的表达式；
(2)点C为线段OB上一动点 （点C不与点O，B重合），作CD∥y轴交直线l2于点D，过点C，D分别向y轴作垂线，垂足分别为F，E，得到矩形CDEF.
①设点C的纵坐标为a，求点D的坐标（用含a的代数式表示）；
②若矩形CDEF的面积为60，请直接写出此时点C的坐标．
【答案】（1）l1的表达式为y=
x，l2的表达式为=－x+24，(2) ①D（3a， －3a＋24）②C（3， 1） 或C(15， 5)
【解析】解：（1）设直线l1的表达式为y=k1x，∵直线l1过B（18， 6），∴18k1=6 ，即k1=。
∴直线l1的表达式为y=x。
设直线l2的表达式为y=k2x+b，∵直线l2过A （0， 24）， B(18， 6)，
∴
解得
y∴直线l2的表达式为=－x+24。
（2） ①∵点C在直线l1上， 且点C的纵坐标为a，
∴a=
x，得x=3a。 ∴点C的坐标为 （3a， a）。
∵CD∥y轴，∴点D的横坐标为3a 。
∵点D在直线l2上 ，∴y=－3a+24。∴D（3a， －3a＋24）。
②C（3， 1） 或C(15， 5)。
（1）设直线l1的表达式为y=k1x，它过（18，6）可求出k1的值，从而得出其解析式；设直线l2的表达式为y=k2+b，由于它过点A（0，24），B（18，6），故把此两点坐标代入即可求出k2，b的值，从而得出其解析式。
（2）①因为点C在直线l1上，且点C的纵坐标为a，故把y=a代入直线l1的表达式即可得出x的值，从而得出C点坐标；由于CD∥y轴，所以点D的横坐标为3a，再根据点D在直线l2上即可得出点D的纵坐标，从而得出结论。
②先根据C、D两点的坐标用a表示出CF及CD的值，由矩形的面积为60即可求出a的值，得出C点坐标：
∵C（3a，a），D（3a，－3a＋24），∴CF=3a，CD=－3a＋24－a=－4a＋24。
∵矩形CDEF的面积为60，∴S矩形CDEF=CFCD=3a×（－4a+24）=60，解得a=1或a=5
当a=1是，3a=3，故C（3，1）；当a=5时，3a=15，故C（15，5）。
综上所述C点坐标为：C（3，1）或C（15，5）。
