��Ŀ����
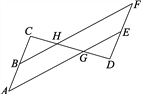
����Ŀ����ͼ��ʾ����֪B��E�ֱ����߶�AC��DF���е㣬AC=DF��BF��CD�ڵ�H��AE��CD�ڵ�G��CH=HG=DG��BH=GE.
(1)��գ���ΪB��E�ֱ����߶�AC��DF���е㣬����CB=________AC��DE=________DF.��ΪAC=DF������CB=________.����CBH����DEG�У���ΪCB=________��CH=________��BH=________EG������________��________(SSS)��
(2)����(1)�е�ȫ���������⣬������д������һ��ȫ�������Σ���˵�����ɣ�
���𰸡�(1) ![]() ��
�� ![]() ��DE��DE��DG����CBH����DEG.����2��֤��������.
��DE��DE��DG����CBH����DEG.����2��֤��������.
�������������������1����ΪB��AC���е㣬 ![]() ͬ��
ͬ��![]() ��ΪAC=DF������֪
��ΪAC=DF������֪![]() ����������ã�
����������ã� ![]() ���ɵá�CBH�ա�DEG.���������ζ�Ӧ��������ȣ�������������ȫ�ȣ������ҳ������ζ�Ӧ������
���ɵá�CBH�ա�DEG.���������ζ�Ӧ��������ȣ�������������ȫ�ȣ������ҳ������ζ�Ӧ������
��2������������������������SAS��֤������
�����������1����ΪB��AC���е㣬 ![]() ͬ��
ͬ��![]()
��ΪAC=DF������֪![]() ����������ã�
����������ã�
![]() ���ɵá�CBH�ա�DEG.
���ɵá�CBH�ա�DEG.
�ʴ�Ϊ�� ![]() ��
�� ![]() ��DE��DE��DG����CBH����DEG.
��DE��DE��DG����CBH����DEG.
(2)��AGC�ա�FHD.
���ɣ���Ϊ��CBH�ա�DEG��
���ԡ�C=��D.��ΪCH=HG=DG��
����CG=DH.
�ڡ�AGC�͡�FHD�У�
��ΪAC=FD����C=��D��CG=DH��
���ԡ�AGC�ա�FHD(SAS)��