题目内容
【题目】在平面直角坐标系中,我们定义点P(a ,b )的“伴随点”为Q,且规定:当a ≥ b时,Q为( b,-a );当 a<b 时,Q为( a,-b).
(1)点(2,1)的伴随点坐标为__________;
(2)若点A(a ,2)的伴随点在函数y=![]() 的图像上,求a的值;
的图像上,求a的值;
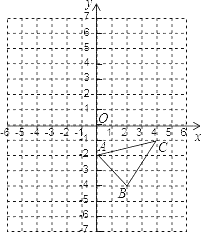
(3)已知直线l与坐标轴交于(6,0),(0,3)两点.将直线l上所有点的伴随点组成一个新的图形记作M.请直接写出直线y=—x+c与图形M有交点时相应的c的取值范围为__________.
【答案】 (1,—2) c≤0
【解析】(1)根据“伴随点”的定义直接写出答案即可;(2)分两种情况求a的值即可;(3)先求得直线l的解析式,再求得当x与y值相等时点C的坐标,根据“伴随点”的定义求得新的图形M是以![]() 为端点的两条射线组成的图形,再确定c的取值范围即可.
为端点的两条射线组成的图形,再确定c的取值范围即可.
(1)(1,—2);
(2)当a≥2时,“伴随点”为(2,—a),则—2 a=1,a=![]() (舍);
(舍);
当a<2时,“伴随点”为(a,—2),则a=![]() ;
;
(3)设直线l的解析式为y=kx+b,将点(6,0)、(0,3)代入y=kx+b,得:
![]() ,
,
解得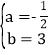 ,
,
∴直线l的解析式为![]()
当x=y时,![]() ,解得x=2;
,解得x=2;
点C的坐标为(2,-2),点C的“伴随点”的坐标为![]() ,
,
点(6,0)的“伴随点”的坐标为(0,-6),点(0,3)的“伴随点”的坐标为(0,-3),
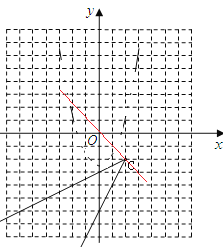
当x≥2时,所有“伴随点”组成的图形是以![]() 为端点,过(0,-6)的一条射线;即:y=2x-6,其中x≥2;
为端点,过(0,-6)的一条射线;即:y=2x-6,其中x≥2;
当x<2时,所有变换点“伴随点”组成的图形是以![]() 为端点,过(0,-3)的一条射线,即
为端点,过(0,-3)的一条射线,即![]() ,其中,x<2;
,其中,x<2;
所以新的图形M是以![]() 为端点的两条射线组成的图形(如图).
为端点的两条射线组成的图形(如图).
因直线y=—x+c与图形M有交点,把![]() 代入y=—x+c可求得c=0,
代入y=—x+c可求得c=0,
∴直线y=—x+c与图形M有交点时c的取值范围为:c≤0.
 .
.