Question

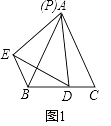
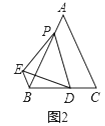
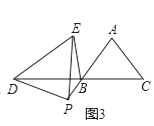
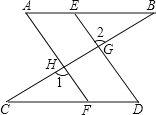
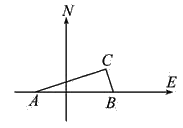
【题目】如图,△ABC、△ADE均为是顶角为42的等腰三角形,BC和DE分别是底边,图中△_________与△___________,可以通过以点________为旋转中心,旋转角度为______．

Answer 1

【答案】ABD ACE A 42°

【解析】

根据已知条件可以证明△ABD≌△ACE，观察图形再根据旋转的概念即可确定旋转中心，旋转角度.

∵△ABC、△ADE均为是顶角为42的等腰三角形，BC和DE分别是底边，

∴AB=AC，AD=AE，∠BAC=∠DAE=42°，

∴∠BAC-∠DAC=∠DAE-∠DAC，

即∠BAD=∠CAE，

∴△BAD≌△CAE，

∴图中△ABD可以通过旋转得到△ACE，旋转中心为A，旋转角度为42°，

故答案为：ABD，ACE，A， 42°.