题目内容
【题目】已知直线y＝x+4分别交x轴、y轴于A、B两点，抛物线y＝x2+mx﹣4经过点A，和x轴的另一个交点为C．
（1）求抛物线的解析式；
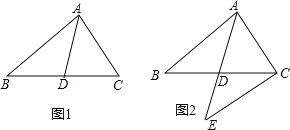
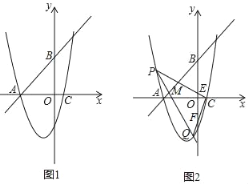
（2）如图1，点D是抛物线上的动点，且在第三象限，求△ABD面积的最大值；
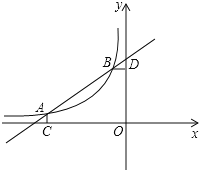
（3）如图2，经过点M（﹣4，1）的直线交抛物线于点P、Q，连接CP、CQ分别交y轴于点E、F，求OEOF的值．
【答案】（1）y＝x2+3x﹣4；（2）当n＝﹣2时，△ABD面积的最大，最大值为24；（3）1.
【解析】
（1）先求得点A的坐标，然后将点A的坐标代入抛物线的解析式求得m的值即可；
（2）设D（n，n2+3n-4），根据图形的面积公式得到S△ABD=-2（n+2）2+24，当n=-2时，求得△ABD最大值为24；
（3）先求得点C的坐标，然后设直线CQ的解析式为y=ax-a，CP的解析式为y=bx-b，接下来求得点Q和点P的横坐标，然后设直线PQ的解析式为y=x+d，把M（-4，1）代入得：y=kx+4k+1，将PQ的解析式为与抛物线解析式联立得到关于x的一元二次方程，然后依据一元二次方程根与系数的关系可求得ab=1，最后，由ab的值可得到OEOF的值．
（1）把y＝0代入y＝x+4得：0＝x+4，解得：x＝﹣4，
∴A（﹣4，0）．
把点A的坐标代入y＝x2+mx﹣4得：m＝3，
∴抛物线的解析式为y＝x2+3x﹣4；
（2）如图1，
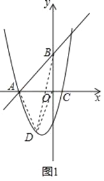
设D（n，n2+3n﹣4），
∴S△ABD＝S四边形ADOB﹣S△BDO＝
×4×4+×4[﹣（n2+3n﹣4）]﹣×4n＝﹣2n2﹣8n+16＝﹣2（n+2）2+24，
∴当n＝﹣2时，△ABD面积的最大，最大值为24；
（3）把y＝0代入 y＝x2+3x﹣4，得：x2+3x﹣4＝0，解得：x＝1或x＝﹣4，
∴C（1，0），
设直线CQ的解析式为y＝ax﹣a，CP的解析式为y＝bx﹣b．
∴
，解得：x＝﹣1或x＝4﹣a，
∴xQ＝4﹣a
同理：xP＝4﹣b，
设直线PQ的解析式为y＝kx+b，把M（﹣4，1）代入得：y＝kx+4k+1．
∴
，
∴x2+（3﹣k）x﹣4k﹣5＝0，
∴xQ+xP＝4﹣a+4﹣b＝3﹣k，xQxP＝（4﹣a）（4﹣b）＝﹣4k﹣5，
解得：ab＝﹣1．
又∵OE＝﹣b，OF＝a，
∴OEOF＝﹣ab＝1．
