��Ŀ����
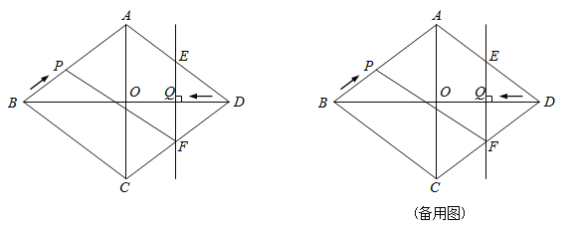
����Ŀ����֪����ͼ������ABCD�����Խ���AC��BD�ཻ�ڵ�O����AC��12cm��BD��16cm����P�ӵ�B��������BA���������˶����ٶ�Ϊ1cm/s��ͬʱ��ֱ��EF�ӵ�D��������DB���������˶����ٶ�Ϊ1cm/s��EF��BD������AD��BD��CD�ֱ��ڵ�E��Q��F����ֱ��EFֹͣ�˶�ʱ����PҲֹͣ�˶�������PF�����˶�ʱ��Ϊt��s����0��t��8�����������������
��1����tΪ��ֵʱ���ı���APFD��ƽ���ı�����
��2�����ı���APFE�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹS�ı���APFE��S����ABCD��17��40�������������t��ֵ���������ʱP��E�����ľ�����������������˵��������
���𰸡���1�� ��t=![]() sʱ���ı���APFD��ƽ���ı��Σ���2��y=-
sʱ���ı���APFD��ƽ���ı��Σ���2��y=-![]() t2+
t2+![]() t+48����3�� PE=
t+48����3�� PE=![]() ��cm����
��cm����
��������
���⣨1�������ı���ABCD�����Σ�OA=![]() AC��OB=
AC��OB=![]() BD����Rt��AOB�У����ù��ɶ������AB=10��������DFQ�ס�DCO���ó�
BD����Rt��AOB�У����ù��ɶ������AB=10��������DFQ�ס�DCO���ó�![]() �����DF����AP=DF�����t��
�����DF����AP=DF�����t��
��2������C��CG��AB�ڵ�G����S����ABCD=ABCG=![]() ACBD�����CG����S����APFD=
ACBD�����CG����S����APFD=![]() ��AP+DF��CG��S��EFD=
��AP+DF��CG��S��EFD=![]() EFQD���ó�y��t֮��ĺ�����ϵʽ��
EFQD���ó�y��t֮��ĺ�����ϵʽ��
��3������C��CG��AB�ڵ�G����S����ABCD=ABCG�����CG����S�ı���APFE��S����ABCD=17��40�����t��������PBN�ס�ABO�����PN��BN�����߶ι�ϵ���EM��PM���ɹ��ɶ������PE��
�����������1�����ı���ABCD�����Σ�
��AB��CD��AC��BD��OA=OC=![]() AC=6�� OB=OD=
AC=6�� OB=OD=![]() BD=8��
BD=8��
��Rt��AOB��AB=10
��EF��BD��
���FQD=��COD=90����
���ߡ�FDQ=��CDO��
���DFQ�ס�DCO��
��![]() ����
����![]()
��DF=![]()
���ı���APFD��ƽ���ı��Σ�
��AP=DF��
��10-t=![]()
��������̣���t=![]() ��
��
����t=![]() sʱ���ı���APFD��ƽ���ı��Σ�
sʱ���ı���APFD��ƽ���ı��Σ�
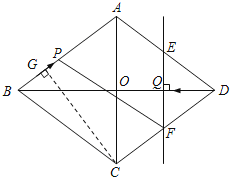
��2����ͼ������C��CG��AB�ڵ�G��
��S����ABCD=ABCG=![]() ACBD��
ACBD��
��10CG=![]() ��12��16��
��12��16��
��CG=![]()
��S����APFD=![]() ��AP+DF��CG
��AP+DF��CG
=![]() ��10-t+
��10-t+![]() ��
��![]()
=![]() t+48��
t+48��
�ߡ�DFQ�ס�DCO��
��![]()
��![]()
��QF=![]() ��
��
ͬ����EQ=![]()
��EF=QF+EQ=![]() ��
��
��S��EFD=![]() EFQD=
EFQD=![]() ��
��![]() ��t=
��t=![]() ��
��
��y=��![]() t+48��-
t+48��-![]() =-
=-![]() +
+![]() t+48��
t+48��
��3����ͼ������P��PM��EF�ڵ�M��PN��BD�ڵ�N��

��S�ı���APFE��S����ABCD=17��40��
��-![]() +
+![]() t+48=
t+48=![]() ��96��
��96��
��5t2-8t-48=0��
��������̣���t1=4��t2=-![]() ����ȥ��
����ȥ��
����P��PM��EF�ڵ�M��PN��BD�ڵ�N��
��t=4ʱ��
�ߡ�PBN�ס�ABO��
��![]()
��![]()
��PN=![]() ��BN=
��BN=![]()
��EM=EQ-MQ=3-![]() =
=![]()
PM=BD-BN-DQ=16-![]() -4=
-4=![]()
��Rt��PME��
PE=![]() cm.
cm.

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�