题目内容
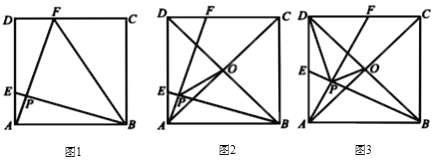
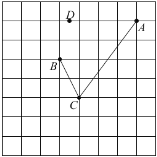
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=4,点P是CB边上的一点,且tan∠PAC=![]() ,⊙O是△APB的外接圆.
,⊙O是△APB的外接圆.
(1)求证:∠PAC=∠ABC;
(2)求证:AC是⊙O的切线;
(3)求⊙O的半径.

【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)通过证明△ACP∽△BCA,可得∠PAC=∠ABC;
(2)作直径AD,交⊙O于点D,连结PD,由圆周角定理可求∠PDA=∠PAC=∠ABC,可证AD⊥AC,即可得⊙O与直线AC的位置关系;
(3)利用锐角三角函数可求CP,PD的长,由勾股定理可求AP的长,AD的长,可得⊙O的半径.
解:(1)证明:在Rt△ACP中,tan∠PAC=![]() =
=![]() ,
,
∵AC=2,BC=4,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠PCA=∠ACB=90°,
∴△ACP∽△BCA,
∴∠PAC=∠ABC;
(2)证明:如图,作⊙O的直径AD,交⊙O于点D,连接PD,
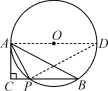
∵AD为⊙O的直径,
∴∠APD=90°,
∴∠PAD+∠PDA=90°,
∵∠PDA=∠ABC,∠PAC=∠ABC,
∴∠PDA=∠PAC,
∴∠PAC+∠PAD=90°,
∴∠CAD=90°,
∴AD⊥AC,
∵AD为⊙O的直径,
∴AC是⊙O的切线;
(3)∵tan∠PAC=![]() =
=![]() ,AC=2,
,AC=2,
∴PC=1,
∴AP=![]() =
=![]()
∵∠PDA=∠PAC,
∴tan∠PAC=tan∠PDA=![]() =
=![]() ,
,
∴PD=2AP=![]() ,
,
∴AD=![]() ,
,
∴⊙O的半径为![]() .
.

【题目】阅读对学生的成长有着深远的影响.某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调查结果经制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A |
| 6 |
|
B |
|
|
|
C |
| 10 |
|
D |
| 8 |
|
E |
| 4 |
|
合计 | 1 |
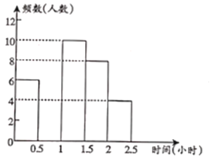
请根据图表中的信息,解答下列问题:
(1)表中的![]() ,
,![]() ,将频数分布直方图补全;
,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足1小时的学生大约有多少名?
(3)![]() 组的4人中,有1名男生和3名女生,该校计划在
组的4人中,有1名男生和3名女生,该校计划在![]() 组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.
组学生中随机选出两人向全校同学作读书心得报告,求抽取的两名学生刚好是1名男生和1名女生的概率.