题目内容
【题目】如图,已知△ABC的三边长为a、b、c,且a<b<c,若平行于三角形一边的直线l将△ABC的周长分成相等的两部分.设图中的小三角形①、②、③的面积分别为S1 , S2 , S3 , 则S1 , S2 , S3的大小关系是 (用“<”号连接)
【答案】S1<S3<S2
【解析】解:设△ABC的面积为S,周长为C.
①若l∥BC,如图1,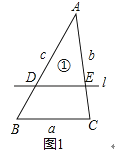
则有△ADE∽△ABC,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ;
;
②若l∥BC,如图2,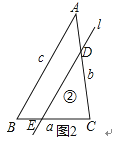
同理可得:![]() =
=![]() ;
;
③若l∥AC,如图3,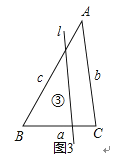
同理可得:![]() =
=![]() .
.
∵0<a<b<c,
∴0<a+b<a+c<b+c,
∴![]() <
<![]() <
<![]() ,
,
∴S1<S3<S2 ,
所以答案是S1<S3<S2 .
设△ABC的面积为S,周长为C.①若l∥BC,如图1,则有△ADE∽△ABC,根据相似三角形的性质及等比性质可得![]() =
=![]() =
=![]() =
=![]() =
=![]() ;②若l∥BC,如图2,同理可得
;②若l∥BC,如图2,同理可得![]() =
=![]() ;③若l∥AC,如图3,同理可得
;③若l∥AC,如图3,同理可得![]() =
=![]() 由0<a<b<c可得0<a+b<a+c<b+c,即可得到
由0<a<b<c可得0<a+b<a+c<b+c,即可得到![]() <
<![]() <
<![]() .
.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目





