Question

【题目】如图，已知⊙O的直径AB=12cm，AC是⊙O的弦，过点C作⊙O的切线交BA的延长线于点P，连接BC．

（1）求证：∠PCA=∠B
（2）已知∠P=40°，点Q在优弧ABC上，从点A开始逆时针运动到点C停止（点Q与点C不重合），当△ABQ与△ABC的面积相等时，求动点Q所经过的弧长。

Answer 1

【答案】
（1）

证明：连接OC，

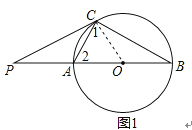
∵PC是⊙O的切线，

∴∠PCO=90°，

∴∠1+∠PCA=90°，

∵AB是⊙O的直径，

∴∠ACB=90°，

∴∠2+∠B=90°，

∵OC=OA，

∴∠1=∠2，

∴∠PCA=∠B；

（2）

解：∵∠P=40°，

∴∠AOC=50°，

∵AB=12，

∴AO=6，

当∠AOQ=∠AOC=50°时，△ABQ与△ABC的面积相等，

∴点Q所经过的弧长==，

当∠BOQ=∠AOC=50°时，即∠AOQ=130°时，△ABQ与△ABC的面积相等，

∴点Q所经过的弧长==，

当∠BOQ=50°时，即∠AOQ=230°时，△ABQ与△ABC的面积相等，

∴点Q所经过的弧长==，

∴当△ABQ与△ABC的面积相等时，动点Q所经过的弧长为或或．

【解析】（1）证明：连接OC，由PC是⊙O的切线，得到∠1+∠PCA=90°，由AB是⊙O的直径，得到∠2+∠B=90°，于是得到结论；
（2）当∠AOQ=∠AOC=50°时，△ABQ与△ABC的面积相等，求得点Q所经过的弧长==，当∠BOQ=∠AOC=50°时，即∠AOQ=130°时，△ABQ与△ABC的面积相等，求得点Q所经过的弧长==，当∠BOQ=50°时，即∠AOQ=230°时，△ABQ与△ABC的面积相等，
∴点Q所经过的弧长==
此题考查了圆的应用，包括切线的性质和弧长的计算。注意分情况讨论，熟练掌握弧长公式。