题目内容
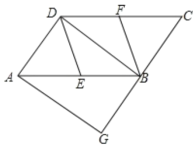
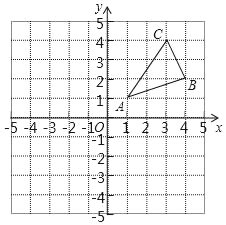
【题目】如图1，抛物线C1：y＝ax2+k的顶点A（0，﹣2），且过点（2，0），点B的坐标为（1，0），直线AB交抛物线C1于另一点C．
（1）抛物线的解析式为 ；
（2）求点C的坐标：
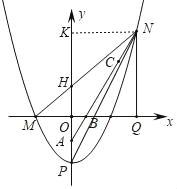
（3）如图2，将抛物线C1向下平移m（m＞0）个单位得到抛物线C，且抛物线C的顶点为P，交x轴负半轴于点M，交射线BC于点N，NQ⊥x轴于点Q，当NP平分∠MNQ时，求m的值．
【答案】（1）y＝
x2﹣2；（2）C（4，6）；（3）2.
【解析】
（1）根据抛物线过点A求出k法人值，再根据线上的另一点（2，0）求出a，将求得的a与k代入，求得解析式
（2）先利用A、B两点坐标，以待定系数法求出直线AB的解析式，再利用方程组求得两个函数图像的交点坐标，根据实际情况判断出交点坐标的正确取值范围即可
（3）分别设出抛物线C2表达式为：y＝
x2﹣2﹣m，点M坐标为（n，0），则C2表达式
为：y＝x2﹣n2，结合（2）中求出的直线AB的表达式得出点N（2﹣n，2﹣2n），从而知道△MNQ为等腰直角三角形；再设直线MN与y轴的交点为H，并作NK⊥y轴于点K，进一步得出NH＝HP，再建立方程求出n从而得出m的值
解：（1）抛物线C1：的顶点A（0，﹣2），则k＝﹣2，
则y＝ax2﹣2，将点（2，0）代入上式得：0＝a（2）2﹣2，
解得：a＝，
则抛物线的表达式：y＝x2﹣2…①，
故答案为：y＝x2﹣2；
（2）将点A、B的坐标代入y＝kx+b得
，解得：
，
故直线AB的表达式为：y＝2x﹣2…②，
联立①②并解得：x＝0或4（舍去0），
故点C（4，6）；
（3）设抛物线C2表达式为：y＝x2﹣2﹣m，设点M（n，0），
则n2﹣2﹣m＝0，抛物线C2表达式为：y＝x2﹣n2…③，
联立②③并解得：x＝2﹣n或2+n，则点N（2﹣n，2﹣2n），
则NQ＝2﹣2n，MQ＝2﹣2n，
∴△MNQ为等腰直角三角形，则∠MNQ＝45°，
又点P（0，﹣n2），即点M（n，0），
设直线MN与y轴的交点为H，则OH＝OM，则点H（0，﹣n），
作NK⊥y轴于点K，在△NKH中，NK＝KH，
则NH＝
（2﹣n），又HP＝OH+OP＝n2﹣n，
∵PN为角平分线，则∠MNP＝∠PNQ＝22.5°，
故NH＝HP，
则（2﹣n）＝n2﹣n，
解得：n＝2或﹣2（舍去2），
∵n2﹣2﹣m＝0，解得：m＝2．
