Question

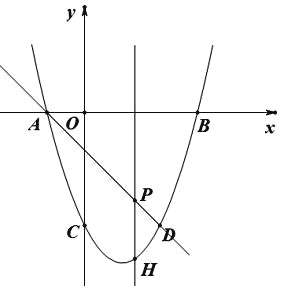
【题目】如图，平面直角坐标系中，点都在轴上，点都在直线上，，且，分别是以为直角顶点的等腰直角三角形，则的面积是_______．

Answer 1

【答案】

【解析】

根据OA1=1，可得点A1的坐标为（1，0），然后根据△B1A1A2，△B2B1A2，△B2A2A3，△B3B2A3…都是等腰直角三角形，求出A1A2，B1A2，A2A3，B2A3…的长度，然后找出规律，求出的面积即可．

∵OA1=1，

∴点A1的坐标为（1，0），

∵△B1A1A2是等腰直角三角形，

∴A1B1= A1A2 =OA1=1，

∴B1（1，1），B1A2= ，

∵△B2B1A2为等腰直角三角形，

∴A2A3=2，B2（2，2），

同理可得，B3（22，22），B4（23，23），…B10（29，29），

∴，

∴.

故答案为．