题目内容
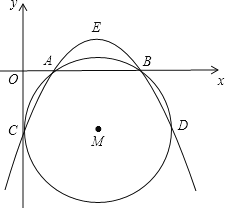
【题目】如图,在直角坐标系中,抛物线y=a(x-![]() )2+
)2+![]() 与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
与⊙M交于A,B,C,D四点,点A,B在x轴上,点C坐标为(0,-2).
(1)求a值及A,B两点坐标;
(2)点P(m,n)是抛物线上的动点,当∠CPD为锐角时,请求出m的取值范围;
(3)点E是抛物线的顶点,⊙M沿CD所在直线平移,点C,D的对应点分别为点C′,D′,顺次连接A,C′,D′,E四点,四边形AC′D′E(只要考虑凸四边形)的周长是否存在最小值?若存在,请求出此时圆心M′的坐标;若不存在,请说明理由.
【答案】(1)A(1,0),B(4,0).(2)m<0或1<m<4或m>5.(3)存在.M′(![]() ,-2)
,-2)
【解析】
(1)把点C坐标代入抛物线解析式即可求出a,令y=0可得抛物线与x轴的交点坐标.
(2)根据题意可知,当点P在圆外部的抛物线上运动时,∠CPD为锐角,由此即可解决问题.
(3)存在.如图2中,将线段C'A平移至D'F,当点D'与点H重合时,四边形AC'D'E的周长最小,求出点H坐标即可解决问题.
解:(1)∵抛物线y=a(x-![]() )2+
)2+![]() 经过点C(0,-2),
经过点C(0,-2),
∴-2=a(0-![]() )2+
)2+![]() ,
,
∴a=-![]() ,
,
∴y=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
当y=0时,-![]() (x-
(x-![]() )2+
)2+![]() =0,
=0,
∴x1=4,x2=1,
∵A、B在x轴上,
∴A(1,0),B(4,0).
(2)由(1)可知抛物线解析式为y=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴C、D关于对称轴x=![]() 对称,
对称,
∵C(0,-2),
∴D(5,-2),
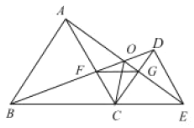
如图1中,连接AD、AC、CD,则CD=5,
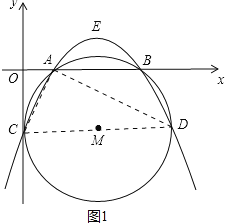
∵A(1,0),C(0,-2),D(5,-2),
∴AC=![]() ,AD=2
,AD=2![]() ,
,
∴AC2+AD2=CD2,
∴∠CAD=90°,
∴CD为⊙M的直径,
∴当点P在圆外部的抛物线上运动时,∠CPD为锐角,
∴m<0或1<m<4或m>5.
(3)存在.如图2中,将线段C′A平移至D′F,则AF=C′D′=CD=5,
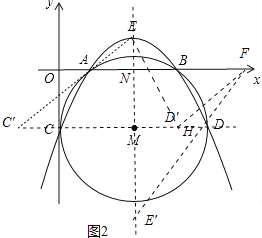
∵A(1,0),
∴F(6,0),
作点E关于直线CD的对称点E′,
连接EE′正好经过点M,交x轴于点N,
∵抛物线顶点(![]() ,
,![]() ),直线CD为y=-2,
),直线CD为y=-2,
∴E′(![]() ,-
,-![]() ),
),
连接E′F交直线CD于H,
∵AE,C′D′是定值,
∴AC′+ED′最小时,四边形AC′D′E的周长最小,
∵AC′+D′E=FD′+D′E=FD′+E′D′≥E′F,
则当点D′与点H重合时,四边形AC′D′E的周长最小,
设直线E′F的解析式为y=kx+b,
∵E′(![]() ,-
,-![]() ),F(6,0),
),F(6,0),
∴可得y=![]() x-
x-![]() ,
,
当y=-2时,x=![]() ,
,
∴H(![]() ,-2),∵M(
,-2),∵M(![]() ,-2),
,-2),
∴DD′=5-![]() =
=![]() ,
,
∵![]() -
-![]() =
=![]() ,
,
∴M′(![]() ,-2)
,-2)

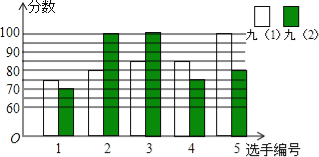
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | 85 | |
九(2) | 80 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.