题目内容
【题目】如图,已知![]() 与
与![]() 是两个全等的直角三角形,量得它们的斜边长为
是两个全等的直角三角形,量得它们的斜边长为![]() ,较小锐角为
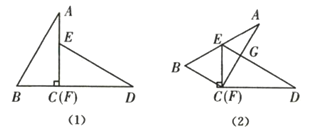
,较小锐角为![]() ,将这两个三角形摆成如图(1)所示的形状,使点
,将这两个三角形摆成如图(1)所示的形状,使点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,且点
在同一条直线上,且点![]() 与点
与点![]() 重合,将图(1)中的
重合,将图(1)中的![]() 绕点
绕点![]() 顺时针方向旋转到图(2)的位置,点
顺时针方向旋转到图(2)的位置,点![]() 在边
在边![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长为______
的长为______![]() .(保留根号)
.(保留根号)
【答案】![]()
【解析】
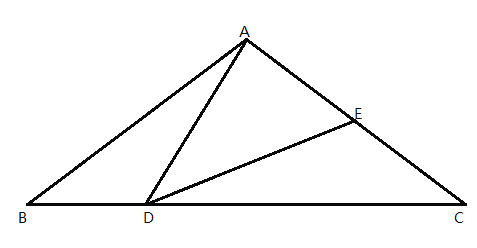
根据直角三角形两锐角互余求出∠B=∠DEF=60°,再根据旋转的性质可得BC=CE,然后判断出△BCE是等边三角形,根据等边三角形的性质可得∠BCE=60°,然后求出∠EFG=30°,再求出∠EGF=90°,根据直角三角形30°角所对的直角边等于斜边的一半求出EF,EG,然后利用勾股定理列式计算即可得FG的长.
解:∵△ACB与△DFE全等,较小锐角为30°,
∴∠B=∠DEF=90°-30°=60°,
由旋转的性质得,BC=CE,
∴△BCE是等边三角形,
∴∠BCE=60°,
∴∠EFG=90°-60°=30°,
∴∠EGF=180°-30°-60°=90°,
∵斜边长为10cm,
∴EF=![]() DE=
DE=![]() ×10=5cm,
×10=5cm,
EG=![]() EF=
EF=![]() ×5=
×5=![]() cm,
cm,
在Rt△EFG中,FG=![]() =
=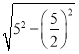 =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目