题目内容
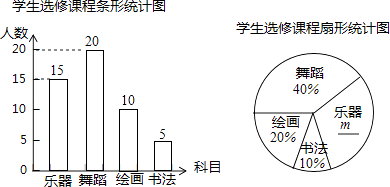
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题: 
(1)本次调查的学生共有人,在扇形统计图中,m的值是;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
【答案】
(1)50;30%
(2)解:50×20%=10(人)
50×10%=5(人)
 .
.
(3)解:∵5﹣2=3(名),
∴选修书法的5名同学中,有3名男同学,2名女同学,
男 | 男 | 男 | 女 | 女 | |
男 | / | (男,男) | (男,男) | (男,女) | (男,女) |
男 | (男,男) | / | (男,男) | (男,女) | (男,女) |
男 | (男,男) | (男,男) | / | (男,女) | (男,女) |
女 | (女,男) | (女,男) | (女,男) | / | (女,女) |
女 | (女,男) | (女,男) | (女,男) | (女,女) | / |
所有等可能的情况有20种,所抽取的2名同学恰好是1名男同学和1名女同学的情况有12种,
则P(一男一女)= ![]() =
= ![]()
答:所抽取的2名同学恰好是1名男同学和1名女同学的概率是 ![]()
【解析】解:(1)20÷40%=50(人)
15÷50=30%
答:本次调查的学生共有50人,在扇形统计图中,m的值是30%.
此题主要考查了扇形统计图和条形统计图的综合运用,要熟练掌握,解答此题的关键是从两种统计图中获取信息并利用获取的信息解题,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目