题目内容
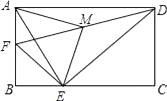
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )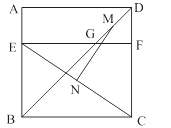
A.3
B.![]()
C.![]()
D.4
【答案】C
【解析】解:取DF、CF中点K、H,连接MK、NH、CM,作MO⊥NH(如下图).
∵四边形ABCD是边长为6的正方形,BE=4.
∴AE=DF=2,CF=BE=4.
∴△DGF∽△BGE
∴![]() =
=![]() =
=![]() .
.
∴GF=2,EF=4.
又∵M、N、K、H、都是中点,
∴MK=![]() GF=1,NH=
GF=1,NH=![]() EF=3.KF=
EF=3.KF=![]() DF=1,FH=
DF=1,FH=![]() CF=2,
CF=2,
∴MK=OH=1.KH=MO=3
∴NO=2.
在Rt△MON中,
∴MN= ![]() =
=![]() =
= ![]() .
.
所以答案是C.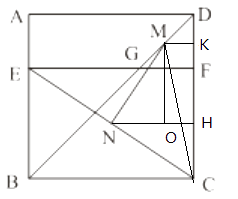
【考点精析】掌握勾股定理的概念和三角形中位线定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
相关题目