题目内容
【题目】如图，在平面直角坐标系中，直线AB经过点A(
，
)和B (2
，0)，且与y轴交于点D，直线OC与AB交于点C，且点C的横坐标为．
(1)求直线AB的解析式；
(2)连接OA，试判断△AOD的形状；
(3)动点P从点C出发沿线段CO以每秒1个单位长度的速度向终点O运动，运动时间为t秒，同时动点Q从点O出发沿y轴的正半轴以相同的速度运动，当点Q到达点D时，P，Q同时停止运动．设PQ与OA交于点M，当t为何值时，△OPM为等腰三角形？求出所有满足条件的t值．
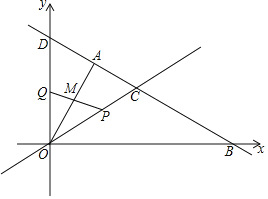
【答案】（1）y＝﹣
x+2；（2）△AOD为直角三角形，理由见解析；（3）t＝
或
．
【解析】
（1）将点A、B的坐标代入一次函数表达式：y＝kx+b，即可求解；
（2）由点A、O、D的坐标得：AD2＝1，AO2＝3，DO2＝4，故DO2＝OA2+AD2，即可求解；
（3）点C（
，1），∠DBO＝30°，则∠ODA＝60°，则∠DOA＝30°，故点C（，1），则∠AOC＝30°，∠DOC＝60°，OQ＝CP＝t，则OP＝2﹣t．①当OP＝OM时，OQ＝QH+OH，即
（2﹣t）+
（2﹣t）＝t，即可求解；②当MO＝MP时，∠OQP＝90°，故OQ＝OP，即可求解；③当PO＝PM时，故这种情况不存在．
解：（1）将点A、B的坐标代入一次函数表达式：y＝kx+b得：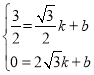 
，
解得：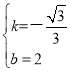
，
故直线AB的表达式为：y＝﹣x+2；
（2）直线AB的表达式为：y＝﹣x+2，则点D（0，2），
由点A、O、D的坐标得：AD2＝1，AO2＝3，DO2＝4，
故DO2＝OA2+AD2，
故△AOD为直角三角形；
（3）直线AB的表达式为：y＝﹣x+2，故点C（，1），则OC＝2，
则直线AB的倾斜角为30°，即∠DBO＝30°，则∠ODA＝60°，则∠DOA＝30°
故点C（，1），则OC＝2，
则点C是AB的中点，故∠COB＝∠DBO＝30°，则∠AOC＝30°，∠DOC＝60°，
OQ＝CP＝t，则OP＝OC﹣PC＝2﹣t，
①当OP＝OM时，如图1，
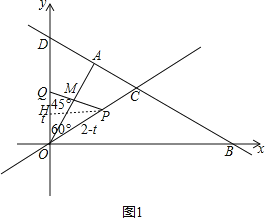
则∠OMP＝∠MPO＝（180°﹣∠AOC）＝75°，故∠OQP＝45°，
过点P作PH⊥y轴于点H，
则OH＝OP＝（2﹣t），
由勾股定理得：PH＝（2﹣t）＝QH，
OQ＝QH+OH＝（2﹣t）+（2﹣t）＝t，
解得：t＝；
②当MO＝MP时，如图2，
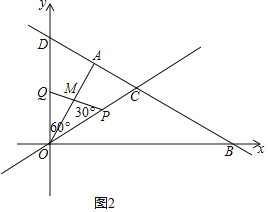
则∠MPO＝∠MOP＝30°，而∠QOP＝60°，
∴∠OQP＝90°，
故OQ＝OP，即t＝（2﹣t），
解得：t＝；
③当PO＝PM时，
则∠OMP＝∠MOP＝30°，而∠MOQ＝30°，
故这种情况不存在；
综上，t＝或．
