题目内容
【题目】如图,等边△ABC中,点D、E、F分别是AB、AC、BC中点,点M在CB的延长线上,△DMN为等边三角形,且EN经过F点.下列结论:①EN=MF ②MB=FN ③MP·DP=NP·FP ④MB·BP=PF·FC,正确的结论有( )
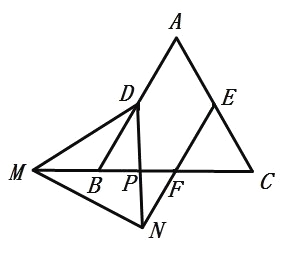
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①连接DE、DF,根据等边三角形的性质得到∠MDF=∠NDE,证明△DMF≌△DNE,根据全等三角形的性质证明;
②根据①的结论结合点D、E、F分别是AB、AC、BC中点,即可得证;
③根据题目中的条件易证得![]() ,即可得证;
,即可得证;
④根据题目中的条件易证得![]() ,再则等量代换,即可得证.
,再则等量代换,即可得证.
连接![]() ,
,

∵![]() 和
和![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∵点![]() 分别为边
分别为边![]() 的中点,
的中点,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∵![]()
![]()
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
故①正确;
∵点![]() 分别为等边三角形三边
分别为等边三角形三边![]() 的中点,
的中点,
∴四边形![]() 为菱形,
为菱形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
故②正确;
∵点![]() 分别为等边三角形三边
分别为等边三角形三边![]() 的中点,
的中点,
∴![]() ∥
∥![]() ,
,
∴![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故③错误;
∵点![]() 分别为等边三角形三边
分别为等边三角形三边![]() 的中点,
的中点,
∴![]() ∥
∥![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由②得![]() ,
,
∴![]() ,
,
∴![]() ,
,
故④正确;
综上:①②④共3个正确.
故选:C

【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示,请根据图表信息解答下列问题:
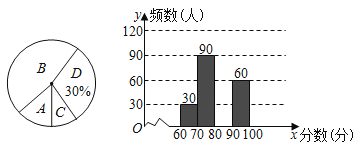
组别 | 分数段(分) | 频数 |
A组 | 60≤x<70 | 30 |
B组 | 70≤x<80 | 90 |
C组 | 80≤x<90 | m |
D组 | 90≤x<100 | 60 |
(1)本次调查的总人数为 人.
(2)补全频数分布直方图;
(3)若A组学生的平均分是65分,B组学生的平均分是75分,C组学生的平均分是85分,D出学生的平均分是95分,请你估计参加本次测试的同学们平均成绩是多少分?
【题目】某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资![]() (结果保留整数),并判断
(结果保留整数),并判断![]() 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.