题目内容
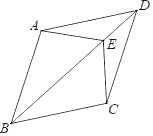
【题目】如图,平行四边形![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,且
,且![]() ,点
,点![]() 为
为![]() 中点,
中点,![]() ,连接
,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
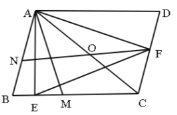
(1)若![]() ,求
,求![]() 的长度;
的长度;
(2)若![]() ,求证
,求证![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由等腰三角形三线合一得AE⊥BM,在Rt△ACE中,求出AE,再在Rt△AEM中求出AM即可;
(2)如图,作EH⊥AF于H,EG⊥DC交DC的延长线于G,由Rt△EHA≌Rt△EGC(HL),推出AH=CG,由Rt△EHF≌Rt△EGF(HL),推出FH=FG,由△AON≌△COF(ASA),推出AN=CF,推出AN+AF=FC+AF=FG-CG+FH+AH=2FH,由EF=![]() FH,即可解决问题
FH,即可解决问题
(1)解: ∵AB=AM,点![]() 为
为![]() 中点,
中点,
∴AE⊥BM,BE=EM=2
在Rt△ACE中,∵AC=![]() ,EC=EM+CM=5,
,EC=EM+CM=5,
∴AE=![]() =
=![]() ,
,
在Rt△AEM中,AM=![]() =
=![]() ;
;
(2)如图,作EH⊥AF于H,EG⊥DC交DC的延长线于G.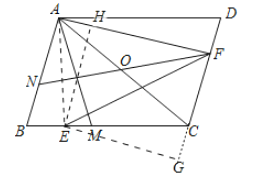
∵平行四边形![]() ,
,
∴AB∥CD,
∵![]()
∴AF⊥CD
∵AE⊥BM,
∵∠AEC=∠AFC=90°,
∵![]() ,
,
∴∠EFA=∠EFG=45°,∠EAC=45°,
∵EH⊥FA,EG⊥FG,
∴EH=EG,
∵∠ACE=∠EAC=45°,
∴AE=EC,
∴Rt△EHA≌Rt△EGC(HL),
∴AH=CG,
∵EF=EF,EH=EG,
∴Rt△EHF≌Rt△EGF(HL),
∴FH=FG,
∵AB∥CD,
∴∠OAN=∠OCF,
∵∠AON=∠COF,OA=OC,
∴△AON≌△COF(ASA),
∴AN=CF,
∴AN+AF=FC+AF=FG-CG+FH+AH=2FH,
∵∠EFA =45°,EH⊥FA,
∴EF=![]() FH,
FH,
∴AN+AF=![]() EF.
EF.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目