��Ŀ����
����Ŀ����ͼ�����κ���y=x2+bx+c��ͼ��x����A��B���㣬��y���ڵ�C������Ϊ��P������B��C�����ֱ��Ϊy=��x+3��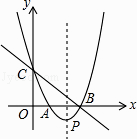
��1����ö��κ����Ĺ�ϵʽ��
��2���ڸ������ߵĶԳ������Ƿ���ڵ�M��ʹ�Ե�C��P��MΪ������������ǵ��������Σ������ڣ���ֱ��д�����з��������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��3������AC����x�����Ƿ���ڵ�Q��ʹ�Ե�P��B��QΪ��������������ABC���ƣ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��ֱ��y=��x+3����B��C���㣬
��B��3��0����C��0��3����
�߶��κ���y=x2+bx+cͼ��x����A��B���㣬��y���ڵ�C��
�� ![]() ���
��� ![]() ��
��
����κ�������ʽΪy=x2��4x+3
��2��
�⣺��y=x2��4x+3=��x��2��2��1��
��������ߵĶԳ���Ϊֱ��x=2����������ΪP��2����1����
����ͼ1��ʾ�����������ĵ�M�ֱ�Ϊ
M1��2��7����M2��2��2 ![]() ��1����M3��2��
��1����M3��2�� ![]() ����M4��2����2
����M4��2����2 ![]() ��1��
��1��

��3��
�⣺�ɣ�1����2����A��1��0����BP= ![]() ��BC=3
��BC=3 ![]() ��AB=2��
��AB=2��
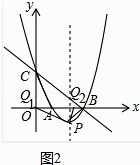
��ͼ2��ʾ������BP����CBA=��ABP=45�㣬
�� ![]() =
= ![]() ʱ����ABC�ס�PBQ1��
ʱ����ABC�ס�PBQ1��
��ʱ�� ![]() =
= ![]() ��
��
��BQ1=3��
��Q1��0��0����
�ڵ� ![]() =
= ![]() ʱ����ABC�ס�Q2BP��
ʱ����ABC�ס�Q2BP��
��ʱ�� ![]() =
= ![]() ��
��
��BQ2= ![]() ��
��
��Q2�� ![]() ��0����
��0����
�������������ڵ�Qʹ���Ե�P��B��QΪ��������������ABC���ƣ�
��Q���꣨0��0���� ![]() ��0����
��0����
����������1�������B��C���꣬���������߽���ʽ�ⷽ���鼴�ɽ�����⣮��2���������������ۼ��ɢ�CM=CP����PM=PC����MP=MC������ͼ�μ��ɽ�����⣮��3���������������ۼ��ɢ� ![]() =
= ![]() ʱ����ABC�ס�PBQ1 �� �г����̼��ɽ�����ڵ�
ʱ����ABC�ס�PBQ1 �� �г����̼��ɽ�����ڵ� ![]() =
= ![]() ʱ����ABC�ס�Q2BP���г����̼��ɽ����
ʱ����ABC�ס�Q2BP���г����̼��ɽ����

����Ŀ����ͼ������ߵ�һ�����ӿ�ʼ����������ÿ��С�����ж�����һ��������ʹ�����������������ڸ�������������֮�Ͷ���ȣ�
6 | a | b | x | -2 | 1 | �� |
��1�������x=______����2016�������е���Ϊ______��
��2���жϣ�ǰm����������������֮���Ƿ����Ϊ2016�����ܣ����m��ֵ���������ܣ���˵�����ɣ�
��3�����x��yΪǰ3�����е���������������ô���е�|x-y|�ĺͿ���ͨ������|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|�õ�����x��yΪǰ20�����е������������������е�|a-b|�ĺ�Ϊ______��