Question

如图，在直角坐标系中，直线AB：y=-

4

3

x+4分别交x、y轴于点A、B，线段OA上的一动点C以每秒1个单位的速度由O向点A运动，线段BA上的一动点D同时以每秒

5

3

个单位的速度由B向A运动．
（1）在运动过程中△ADC与△ABO是否相似？试说明你的理由；
（2）问当运动时间t为多少秒时，以CD为直径的圆与y轴相切？
（3）在运动过程中是否存在某一时刻，使得△OCD与△ACD相似？若存在，求出运动时间；若不存在，说明理由．

Answer 1

分析：（1）先分别求出OA=3，OB=4，则AB=5，设动点C移动的时间为t秒，则AD=5-

5

3

t，AC=3-t，再分别求出AD：AB，AC：AO，可得AD：AB=AC：AO，根据三角形相似的判定方法得到△ADC与△ABO相似；
（2）由（1）得CD⊥OA，通过CD：OB=AC：AO，得到CD=

4

3

（3-t），当CD为直径的圆与y轴相切时，OC等于圆的半径，则CD=2OC，即

4

3

（3-t）=2t，解出t即可；
（3）易知△OCD与△ACD都是直角三角形，分类：当OC：CD=CD：AC时，Rt△OCD∽Rt△DCA；当OC：AC=CD：CD=1，Rt△OCD∽Rt△ACD，然后分别列出t的方程，解方程即可．

解答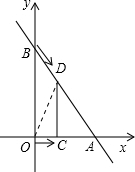：解：（1）在运动过程中△ADC与△ABO相似．理由如下：
对于y=-

4

3

x+4，令x=0，y=4；令y=0，得x=3，
∴OA=3，OB=4，则AB=5，
设动点C移动的时间为t秒，
∴BD=

5

3

t，OC=t，
∴AD=5-

5

3

t，AC=3-t，
∴

AD

AB

=

5- 5 3 t

5

=

3-t

3

，
而

AC

AO

=

3-t

3

，
∴AD：AB=AC：AO，
∴△ADC∽△ABC；

（2）由（1）得CD⊥OA，并且CD：OB=AC：AO，即CD：4=3：（3-t），
∴CD=

4

3

（3-t），
当CD为直径的圆与y轴相切时，OC等于圆的半径，
∴CD=2OC，即

4

3

（3-t）=2t，
∴t=

6

5

（秒），
即当运动时间t为

6

5

秒时，以CD为直径的圆与y轴相切；

（3）存在．理由如下：
△OCD与△ACD都是直角三角形，
∴当OC：CD=CD：AC时，Rt△OCD∽Rt△DCA，
∴

t

4 3 (3-t)

=

4 3 (3-t)

3-t

，解得t=

48

25

；
当OC：AC=CD：CD=1，Rt△OCD∽Rt△ACD，
∴

t

3-t

=1，解得t=

3

2

，
所以运动过程中当时间为

48

25

或

3

2

秒时，可使得△OCD与△ACD相似．

点评：本题考查了求直线与坐标轴的交点坐标的方法．也考查了三角形相似的判定与性质以及直线与圆相切的判定与性质．