题目内容
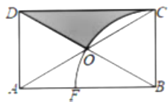
【题目】如图,矩形![]() 中,对角线
中,对角线![]() 、
、![]() 交于
交于![]() ,以
,以![]() 为圆心、
为圆心、![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ,若点
,若点![]() 恰好在圆弧上,且
恰好在圆弧上,且![]() ,则阴影部分的面积为__________.
,则阴影部分的面积为__________.
【答案】![]()
【解析】
根据矩形的性质得到AC=BD,OC=![]() AC,OB=
AC,OB=![]() BD,再由BC和BO是半径推出△OBC是等边三角形,进而得到扇形圆心角∠CBO=60°. 在Rt△ABC中,根据勾股定理列方程,求出BC的长,再根据S阴影=S△DCB-S扇形BOC求解即可.
BD,再由BC和BO是半径推出△OBC是等边三角形,进而得到扇形圆心角∠CBO=60°. 在Rt△ABC中,根据勾股定理列方程,求出BC的长,再根据S阴影=S△DCB-S扇形BOC求解即可.
解:∵四边形ABCD是矩形,
∴AB=CD=![]() ,∠ABC=90°,AC=BD,OC=
,∠ABC=90°,AC=BD,OC=![]() AC,OB=
AC,OB=![]() BD,
BD,
∴OC=OB,
又∵BC=BO,
∴△OBC是等边三角形,
∴∠CBO=60°,AC=2BC.
在Rt△ABC中,AB2+BC2=AC2,
∴(![]() )2+( BC)2=(2 BC)2,
)2+( BC)2=(2 BC)2,
解得:BC=6,
∴S阴影=S△DCB-S扇形BOC=![]() ×6×
×6×![]() -
-![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
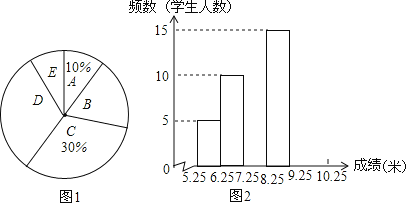
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下尚不完整的统计图表:
组别 | A | B | C | D | E |
分组(元) | 0≤x<30 | 30≤x<60 | 60≤x<90 | 90≤x<120 | 120≤x<150 |
频数 | 4 | a | 20 | 8 | 2 |
请根据以上图标,解答下列问题:
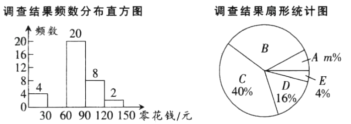
(1)填空:这次调查的样本容量是 ,a= ,m= ;
(2)补全频数分布直方图;
(3)求扇形统计图中扇形B的圆心角度数;
(4)该校共有1000人,请估计每月零花钱的数额x在30≤x<90范围的人数;
【题目】下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差.根据表中数据,要从中选择一名成绩好且发挥稳定的同学参加数学竞赛,应该选择__________(填“甲”, “乙”, “丙”, “丁”).
甲 | 乙 | 丙 | 丁 | |
平均数(分) | 92 | 95 | 95 | 92 |
方差 | 3.6 | 3.6 | 7.4 | 8.1 |