题目内容
若关于x的方程(x-2)(x2-4x+m)=0有三个根,且这三个根恰好可以作为一个三角形的三条边的长,则m的取值范围是分析:根据原方程可知x-2=0,和x2-4x+m=0,因为关于x的方程(x-2)(x2-4x+m)=0有三个根,所以x2-4x+m=0的根的判别式△>0,然后再由三角形的三边关系来确定m的取值范围.
解答:解:∵关于x的方程(x-2)(x2-4x+m)=0有三个根,
∴①x-2=0,解得x1=2;
②x2-4x+m=0,
∴△=16-4m≥0,即m≤4,
∴x2=2+
,
x3=2-
,
又∵这三个根恰好可以作为一个三角形的三条边的长,
且最长边为x2,
∴x1+x3>x2;
解得3<m≤4,
∴m的取值范围是3<m≤4.
故答案为:3<m≤4.
∴①x-2=0,解得x1=2;
②x2-4x+m=0,
∴△=16-4m≥0,即m≤4,
∴x2=2+
| 4-m |
x3=2-
| 4-m |
又∵这三个根恰好可以作为一个三角形的三条边的长,
且最长边为x2,
∴x1+x3>x2;
解得3<m≤4,
∴m的取值范围是3<m≤4.
故答案为:3<m≤4.
点评:本题主要考查了根与系数的关系、根的判别式及三角形的三边关系.解答此题时,需注意,三角形任意两边和大于第三边.

练习册系列答案
相关题目
若关于x的方程(x-2)+3k=
的根是负数,则k的取值范围是( )
| x+k |
| 3 |
A、k>
| ||
B、k≥
| ||
C、k<
| ||
D、k≤
|
若关于x的方程(m-1)xm2+1+5x+2=0是一元二次方程,则m的值等于( )
| A、1 | B、-1 | C、±1 | D、0 |
若关于x的方程3x+a=0的解比方程-
x-4=0的解大2,则a的值( )
| 2 |
| 3 |
| A、-18 | B、12 |
| C、24 | D、-12 |

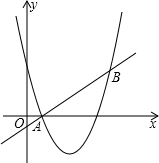 直线y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,且不等式x+a>x2+bx+c 的整数解为K,若关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),求m的值.
直线y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,且不等式x+a>x2+bx+c 的整数解为K,若关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),求m的值.