题目内容
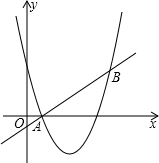 直线y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,且不等式x+a>x2+bx+c 的整数解为K,若关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),求m的值.
直线y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,且不等式x+a>x2+bx+c 的整数解为K,若关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),求m的值.
分析:利用待定系数法首先求出两函数的解析式,再结合图象得出k的值,再利用根与系数的关系求出m的值.
解答:解:∵y=x+a和抛物线y=x2+bx+c都经过A(1,0)、B(3,2)两点,
∴将A(1,0)代入y=x+a,
得:y=x-1,
将A(1,0)、B(3,2)两点,代入抛物线y=x2+bx+c解析式得:
,
解得:b=-3,c=2,
∴抛物线解析式为:y=x2-3x+2,
∵不等式x+a>x2+bx+c 的整数解为K,
即:x-1>x2-3x+2的解集,
结合两图象的交点坐标以及图象即可得出解集,
1<x<3,
∴整数解为K为:2,
∵关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),
∴n=2(K+1)=6,
∵|x1-x2|=6,
∴(x1-x2)2=36,
∴(x1+x2)2-4x1x2=36,
∴(m2+5)2-4(2m2+6)=36,
整理得:m4+2m2-35=0,
解得:m2=5或-7(不合题意舍去),
∴m=±
.
∴将A(1,0)代入y=x+a,
得:y=x-1,
将A(1,0)、B(3,2)两点,代入抛物线y=x2+bx+c解析式得:
|
解得:b=-3,c=2,
∴抛物线解析式为:y=x2-3x+2,
∵不等式x+a>x2+bx+c 的整数解为K,
即:x-1>x2-3x+2的解集,
结合两图象的交点坐标以及图象即可得出解集,
1<x<3,
∴整数解为K为:2,
∵关于x的方程x2-(m2+5)x+2m2+6=0的两实根之差的绝对值为n,且n满足n=2(K+1),
∴n=2(K+1)=6,
∵|x1-x2|=6,
∴(x1-x2)2=36,
∴(x1+x2)2-4x1x2=36,
∴(m2+5)2-4(2m2+6)=36,
整理得:m4+2m2-35=0,
解得:m2=5或-7(不合题意舍去),
∴m=±
| 5 |
点评:此题主要考查了二次函数与一次函数综合题目,利用函数图象判断函数值的大小问题以及利用根与系数的关系进行计算是解决问题的关键也是中考热点题型.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 (2012•济南)如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需
(2012•济南)如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需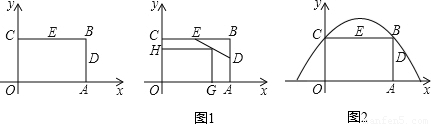
 ,
,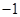 )的抛物线交
)的抛物线交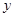 轴于
轴于 点,交
点,交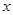 轴于
轴于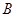 ,
, 两点(点
两点(点 ,
, ).
).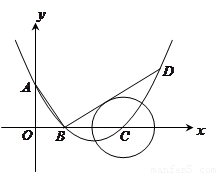
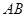 的垂线交抛物线于点
的垂线交抛物线于点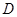 ,
,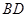 相切,请判断抛物
相切,请判断抛物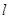 与⊙
与⊙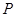 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于 的
的