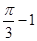题目内容
(8分)如图,在△ABC中,AB=AC,点O为底边上的中点,以点O为圆心,
1为半径的半圆与边AB相切于点D.
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当∠A=60°时,求图中阴影部分的面积.
1为半径的半圆与边AB相切于点D.
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当∠A=60°时,求图中阴影部分的面积.

解:(1)直线AC与⊙O相切.························································· 1分
理由是:
连接OD,过点O作OE⊥AC,垂足为点E.

∵⊙O与边AB相切于点D,
∴OD⊥AB.·························································································· 2分
∵AB=AC,点O为底边上的中点,
∴AO平分∠BAC····················································································· 3分
又∵OD⊥AB,OE⊥AC
∴OD= OE····························································································· 4分
∴OE是 ⊙O的半径.
⊙O的半径.
又∵OE⊥AC,∴直线AC与⊙O相切.·························································· 5分
(2)∵AO平分∠BAC,且∠BAC=60°,∴∠OAD=∠OAE=30°,
∴∠AOD=∠AOE=60°,
理由是:
连接OD,过点O作OE⊥AC,垂足为点E.

∵⊙O与边AB相切于点D,
∴OD⊥AB.·························································································· 2分
∵AB=AC,点O为底边上的中点,
∴AO平分∠BAC····················································································· 3分
又∵OD⊥AB,OE⊥AC
∴OD= OE····························································································· 4分
∴OE是
 ⊙O的半径.
⊙O的半径.又∵OE⊥AC,∴直线AC与⊙O相切.·························································· 5分
(2)∵AO平分∠BAC,且∠BAC=60°,∴∠OAD=∠OAE=30°,
∴∠AOD=∠AOE=60°,
 略
略
练习册系列答案
相关题目
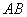 为半圆
为半圆 的直径,延长
的直径,延长 ,使
,使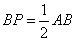 ,
,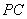 切半圆
切半圆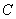 ,点
,点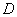 是弧AC上和点
是弧AC上和点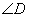 的度数为
的度数为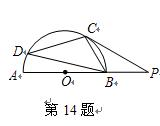
 经过半径为r的⊙O的圆心,⊙O与⊙
经过半径为r的⊙O的圆心,⊙O与⊙




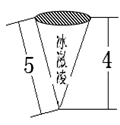




 .
.
 的两根,且O1O2=1,则⊙O1和⊙O2的位置关系是 _________ .
的两根,且O1O2=1,则⊙O1和⊙O2的位置关系是 _________ . 的边
的边 ,
,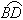 和
和 都是以
都是以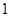 为半径的圆弧,则无阴影
为半径的圆弧,则无阴影