题目内容
【题目】已知关于x的一元二次方程x2+2x+
=0有实数根，k为正整数．
（1）求k的值；
（2）当此方程有两个非零的整数根时，将关于x的二次函数y=x2+2x+的图象向下平移9个单位，求平移后的图象的表达式；
（3）在（2）的条件下，平移后的二次函数的图象与x轴交于点A，B（点A在点B左侧），直线y=kx+b（k＞0）过点B，且与抛物线的另一个交点为C，直线BC上方的抛物线与线段BC组成新的图象，当此新图象的最小值大于﹣5时，求k的取值范围．
【答案】解：（1）∵关于x的一元二次方程x2+2x+
=0有实数根，
∴△=b2﹣4ac=4﹣4×≥0，
∴k﹣1≤2，
∴k≤3，
∵k为正整数，
∴k的值是1，2，3；
（2）∵方程有两个非零的整数根，
当k=1时，x2+2x=0，不合题意，舍去，
当k=2时，x2+2x+
=0，
方程的根不是整数，不合题意，舍去，
当k=3时，x2+2x+1=0，
解得：x1=x2=﹣1，符合题意，
∴k=3，
∴y=x2+2x+1，
∴平移后的图象的表达式y=x2+2x+1﹣9=x2+2x﹣8；
（3）令y=0，x2+2x﹣8=0，
∴x1=﹣4，x2=2，
∵与x轴交于点A，B（点A在点B左侧），
∴A（﹣4，0），B（2，0），
∵直线l：y=kx+b（k＞0）经过点B，
∴函数新图象如图所示，当点C在抛物线对称轴左侧时，新函数的最小值有可能大于﹣5，
令y=﹣5，即x2+2x﹣8=﹣5，
解得：x1=﹣3，x2=1，（不合题意，舍去），
∴抛物线经过点（﹣3，﹣5），
当直线y=kx+b（k＞0）经过点（﹣3，﹣5），（2，0）时，
可求得k=1，
由图象可知，当0＜k＜1时新函数的最小值大于﹣5．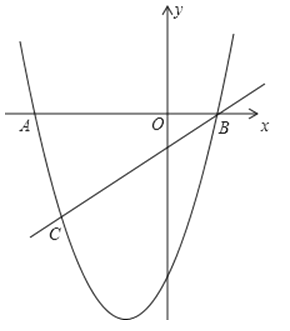
【解析】（1）根据方程有实数根可得△≥0，求出k的取值范围，然后根据k为正整数得出k的值；
（2）根据方程有两个非零的整数根进行判断，得出k=3，然后得出函数解析式，最后根据平移的性质求出平移后的图象的表达式；
（3）令y=0，得出A、B的坐标，作出图象，然后根据新函数的最小值大于﹣5，求出C的坐标，然后根据B、C的坐标求出此时k的值，即可得出k的取值范围．
【考点精析】掌握二次函数的概念是解答本题的根本，需要知道一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数．
