题目内容
【题目】如图,在Rt△ABC中∠C=90°,放置边长分别为4、6、x的三个正方形,则x的值为( )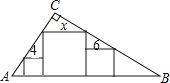
A.24
B.12
C.10
D.8
【答案】C
【解析】解:
∵在Rt△ABC中(∠C=90°),放置边长分别4,6,x的三个正方形,
∴△CEF∽△OME∽△PFN,
∴OE:PN=OM:PF,
∵EF=x,MO=4,PN=6,
∴OE=x﹣4,PF=x﹣6,
∴(x﹣4):6=4:(x﹣6),
∴(x﹣4)(x﹣6)=24,
∴x=0(不符合题意,舍去),x=10.
故选C.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目