题目内容
【题目】如图，在一棵树CD的10m高处的B点有两只猴子，它们都要到A处池塘边喝水，其中一只猴子沿树爬下走到离树20m处的池塘A处，另一只猴子爬到树顶D后直线跃入池塘的A处．如果两只猴子所经过的路程相等，试问这棵树多高？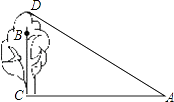 
【答案】解：设BD高为x，则从B点爬到D点再直线沿DA到A点，走的总路程为x+AD，其中AD= 
而从B点到A点经过路程（20+10）m=30m，
根据路程相同列出方程x+ =30，
可得 =30﹣x，
两边平方得：（10+x）2+400=（30﹣x）2 ，
整理得：80x=400，
解得：x=5，
所以这棵树的高度为10+5=15m．
故答案为：15m．
【解析】要求树的高度，就要求BD的高度，在直角三角形ACD中运用勾股定理可以列出方程式，CD2+AC2=AD2 ， 其中CD=CB+BD．
练习册系列答案
导学全程练创优训练系列答案
相关题目
