题目内容
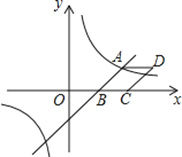
【题目】如图,在直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与直线
两点,与直线![]() 交于点
交于点![]() .
.
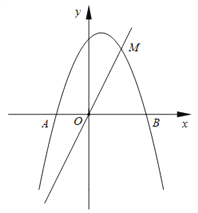
(1)求![]() ,
, ![]() 的值;
的值;
(2)已知点![]() ,点
,点![]() 关于原点
关于原点![]() 对称,现将线段
对称,现将线段![]() 沿
沿![]() 轴向上平移
轴向上平移![]() (
(![]() >0)个单位长度.若线段
>0)个单位长度.若线段![]() 与抛物线有两个不同的公共点,试求
与抛物线有两个不同的公共点,试求![]() 的取值范围;
的取值范围;
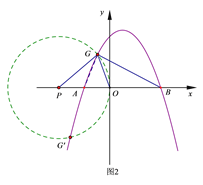
(3)利用尺规作图,在该抛物线上作出点![]() ,使得
,使得![]() ,并简要说明理由.(保留作图痕迹)
,并简要说明理由.(保留作图痕迹)
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() 取值范围为
取值范围为![]() ;(3)作图见解析,理由见解析.
;(3)作图见解析,理由见解析.
【解析】试题分析:(1)、根据一次函数解析求出点M的坐标,然后将点M的坐标代入二次函数解析式得出b的值;(2)、根据对称得出点N的坐标,过点N作CN⊥x轴,交抛物线于C,从而得出CN=AN=2,即当S=2时线段MN与抛物线有两个交点,然后设平移后的解析式为y=2x+s,然后将一次函数和二次函数联立成方程组,根据根的判别式得出s的值,从而得出取值范围;(3)、如图,在x轴上取一点P(-2,0)以P为圆心,OP为半径作圆,⊙P与抛物线的交点,即是所求作的点G,根据△GPA和△BPG相似得出答案.
试题解析:(1)、把![]() 代入
代入![]() 得
得![]()
把![]() 代入
代入![]() 得
得![]() 即
即![]()
(2)、由(1)得![]()
![]()
因为点![]() ,点
,点![]() 关于原点
关于原点![]() 对称,所以
对称,所以![]()
过点N作![]() 轴,交抛物线于C, 则C的横坐标为
轴,交抛物线于C, 则C的横坐标为![]()
所以C的纵坐标为![]() 所以
所以![]() 与
与![]() 重合.
重合.
则![]() ,即当
,即当![]() 线段
线段![]() 与抛物线有两个公共点
与抛物线有两个公共点
设平移后的直线表达式为![]() 由
由![]() 得
得![]()
由![]() 得
得![]() 即当
即当![]() 线段
线段![]() 与抛物线只有一个公共点.
与抛物线只有一个公共点.
所以,当线段![]() 与抛物线有两个公共点时.
与抛物线有两个公共点时. ![]() 取值范围为
取值范围为![]()
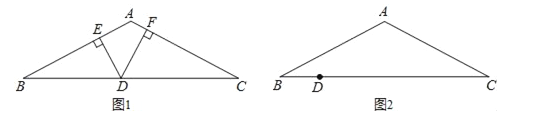
(3)、如图,在![]() 轴上取一点
轴上取一点![]() 以
以![]() 为圆心,
为圆心, ![]() 为半径作圆,⊙
为半径作圆,⊙![]() 与抛物线的交点,即是所求作的点
与抛物线的交点,即是所求作的点![]() (图中的
(图中的![]() 与
与![]() )
)
理由:当点![]() 在
在![]() 轴上方时, 由作图可知,
轴上方时, 由作图可知, ![]()
则![]() 又∵
又∵![]() ∴
∴![]() ∴
∴![]()
∵![]() ∴
∴![]()
又![]()
![]() ∴
∴![]()
同理可证:当点![]() (
(![]() )在
)在![]() 轴下方时,结论也成立.
轴下方时,结论也成立.

练习册系列答案
相关题目