Question

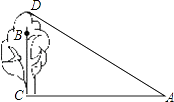
【题目】如图，∠B=42°，∠1=∠2+10°，∠ACD=64°，∠ACD的平分线与BA的延长线相交于点E.

（1）请你判断BF与CD的位置关系，并说明理由；

（2）求∠3的度数.

Answer 1

【答案】（1）BF∥CD；（2）148°

【解析】

试题分析：（1）由∠B=42°，∠1=∠2+10°根据三角形的内角和定理可求得∠2=64°，再结合∠ACD=64°即可证得结论；

（2）根据角平分线的性质可得∠DCE=∠ACD=32°，再根据平行线的性质求解即可.

解：（1）BF∥CD，理由如下：

因为∠B=42°，∠1=∠2+10°，且三角形内角和为180°

所以∠2=64°

又因为∠ACD=64°，所以∠ACD=∠2，因此BF∥CD；

（2）因为CE平分∠ACD，所以∠DCE=∠ACD=32°

因为BF∥CD，所以∠3=180°- 32°=148°.