题目内容
在平面直角坐标系中,正方形ABCD的顶点坐标分别为A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点 P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2013的坐标为 .
(2,0)
如图,点P关于点A的对称点P1(2,0), 点P1关于点B的对称点 P2(0,-2), 点P2关于点C的对称点P3(-2,0), 点P3关于点D的对称点P4(0,2), P4与P重合, P5与P1重合,故对称点以4为一个循环, P1(2,0), P2(0,-2), P3(-2,0), P4(0,2),2013除以4余1,所以P2013与P1重合,故P2013(2,0).

试题分析:先求出几个对称点的坐标,然后找规律,由题,如图,点P关于点A的对称点P1(2,0), 点P1关于点B的对称点 P2(0,-2), 点P2关于点C的对称点P3(-2,0), 点P3关于点D的对称点P4(0,2), P4与P重合, P5与P1重合,故对称点以4为一个循环, P1(2,0), P2(0,-2), P3(-2,0), P4(0,2),2013除以4余1,所以P2013与P1重合,故P2013(2,0).

试题分析:先求出几个对称点的坐标,然后找规律,由题,如图,点P关于点A的对称点P1(2,0), 点P1关于点B的对称点 P2(0,-2), 点P2关于点C的对称点P3(-2,0), 点P3关于点D的对称点P4(0,2), P4与P重合, P5与P1重合,故对称点以4为一个循环, P1(2,0), P2(0,-2), P3(-2,0), P4(0,2),2013除以4余1,所以P2013与P1重合,故P2013(2,0).

练习册系列答案
相关题目
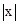 ),则点P一定( )
),则点P一定( )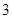 ,
, )关于原点对称的对称点的坐标是( )
)关于原点对称的对称点的坐标是( )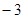 ,
,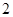 )
)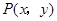 ,满足
,满足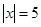 ,
,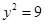 ,则点
,则点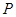 的坐标是 .
的坐标是 .