题目内容
如图,在平面直角坐标系中,△ABC与△A′B′C′关于点P位似,且顶点都在格点上.
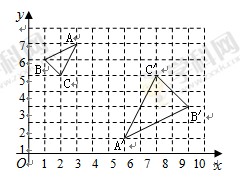
(1)在图上找出位似中心P的位置,并直接写出点P的坐标是 ;
(2)写出△ABC与△A′B′C′的面积比.

(1)在图上找出位似中心P的位置,并直接写出点P的坐标是 ;
(2)写出△ABC与△A′B′C′的面积比.
(1)P的位置见解析,点P的坐标为(4,5);
(2)△ABC与△A′B′C′的面积比为1:4.
(2)△ABC与△A′B′C′的面积比为1:4.
试题分析:(1)连接AA′、BB′,交于点P,求出P坐标即可;
(2)求出边长为1和2的正方形的对角线,得到BC与B′C′的长,求出BC与B′C′的比值,根据三角形ABC与三角形A′B′C′相似,由面积比等于相似比的平方即可求出面积之比.
试题解析:(1)如图:

点P的坐标为(4,5);
(2)由图得:BC=
 ,B′C′=
,B′C′= .所以BC与B′C′的比为1:2,根据三角形ABC与三角形A′B′C′相似,所以△ABC与△A′B′C′的面积比为1:4.
.所以BC与B′C′的比为1:2,根据三角形ABC与三角形A′B′C′相似,所以△ABC与△A′B′C′的面积比为1:4.
练习册系列答案
相关题目
 的三个顶点均在格点上,点A、B的坐标分别为果
的三个顶点均在格点上,点A、B的坐标分别为果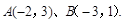

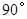 后的
后的 ;
; 的坐标;
的坐标; 的面积.
的面积.