题目内容
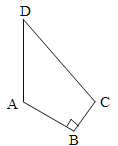
【题目】如图所示，四边形ABCD中，AB=4，BC=3，AD=13，CD=12，∠B=90°，求该四边形的面积．
【答案】36．
【解析】
试题分析：如图所示，连接AC，可得△ABC与△DAC均为直角三角形，进而可求解四边形的面积．
试题解析：连接AC，
因为AB=4，BC=3，CD=13，DA=12，∠B=90°，
所以AC2=AB2-+BC2 ，
=42+32，
=16+9，
=25，
所以AC=5，
又因CD2-DA2，
=132-122，
=169-144，
=25，
=AC2，
所以△DAC为直角三角形，
因此S四边形ABCD的面积=S△ABC+S△DAC，
=
AB×BC+AD×AC，
=×4×3+×12×5，
=6+30，
=36．
答：四边形ABCD的面积等于36．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小宇根据他们的成绩绘制了尚不完整的统计图表（如图），并计算了甲成绩的平均数和方差（见如图小宇的作业）．
甲、乙两人射箭成绩统计表
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
（1）a＝ ；
（2）请完成图中表示乙成绩变化情况的折线．
（3）观察图，可看出 的成绩比较稳定（填“甲”或“乙”）．参照小宇的计算方法，计算乙成绩的方差，并验证你的判断．
