题目内容
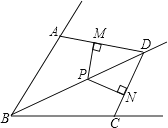
【题目】一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，匀速行驶．设慢车行驶的时间x（h），两车之的距离为y（km），图中的折线表示y与x之间的函数关系．
（1）求慢车和快车的速度；
（2）求线段BC所表示的y与x的函数关系式，并写出自变量x的取值范围；
（3）第一列快车出发后又有一列快车(与第一列快车速度相同)从甲地出发，与慢车同时到达各自的目的地．请直接写出第二列快车出发后经过多少小时与慢车相遇，相遇时他们距甲地的距离．
【答案】（1）
，
；（2）
（
）；（3）经过2小时与慢车相遇，相遇时他们距甲地的距离为300km
【解析】
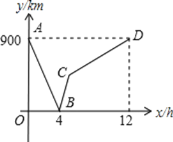
（1）由图可知甲、乙两地之间的距离为900km；两车同时出发后经4h相遇；图中点D的实际意义是：慢车行驶12h到达甲地；可得慢车12h的行程为900km，即可求出慢车速度；两车出发后经4小时相遇，即可求出快车速度．
（2）先求出B、C点坐标，即可求出线段BC所表示的y与x的函数关系式与自变量x的取值范围．
（3）已知第一列快车出发后又有一列快车(与第一列快车速度相同)从甲地出发，与慢车同时到达各自的目的地，得第二列开车速度为150(km/h)，设第二列快车与慢车相遇时，距离甲地为x米，
，解得x=300，快车出发后
小时，与慢车相遇．
∵甲、乙两地之间的距离为900km；
两车同时出发后经4h相遇；
图中点D的实际意义是：慢车行驶12h到达甲地；
∴慢车12h的行程为900km，所以速度为：900÷12=75(km/h)，
∵两车出发后经4小时相遇，
∴快车速度为：900÷475=150(km/h)；
故答案为：150(km/h)，75(km/h)
（2）∵B(4,0)，快车速度为：150km/h，
∴900÷150=6(小时)，
C点纵坐标为：75×6=450，
∴C(6,450)，
设线段BC表示的关系为：y=kx+b(4x6)，
∴
解得：k=225，b=900
∴线段BC的函数表达式为：y=225x900(4x6)；
故答案为：y=225x900(4x6)
（3）∵第一列快车出发后又有一列快车(与第一列快车速度相同)从甲地出发，与慢车同时到达各自的目的地
∴第二列开车速度为150(km/h)
设第二列快车与慢车相遇时，距离甲地为x米，
∵第二列快车与慢车同时到达各自的目的地
∴
解得x=300
∴快车出发后小时，与慢车相遇．
故答案为：经过2小时与慢车相遇，相遇时他们距甲地的距离为300km
阅读快车系列答案
【题目】一辆小汽车在高速公路上从静止到起动10秒内的速度经测量如下表：
时间（秒） | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
速度（米/秒） | 0 | 0.3 | 1.3 | 2.8 | 4.9 | 7.6 | 11.0 | 14.1 | 18.4 | 24.2 | 28.9 |
（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
（2）如果用T表示时间，V表示速度，那么随着T的变化，V的变化趋势是什么？
（3）当T每增加1秒，V的变化情况相同吗？在哪1秒钟，V的增加最大？
（4）若高速公路上小汽车行驶速度的上限为120千米/小时，试估计大约还需几秒这辆小汽车的速度就将达到这个上限。
【题目】近年来，随着电子商务的快速发展，电商包裹件总量占当年快递件总量的比例逐年增长.根据某快递公司某网点的数据统计，得到如下统计表：
快递件总量与电商包裹件总量数据统计表
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
快递件总量（万件） | 1.8 | 2 | 3.1 | 4.5 | 6 |
电商包裹件总量（万件） | 1.296 | 1.48 | 2.356 | 3.555 | 4.86 |
电商包裹件总量占当年快递件总量的百分比（%） | 72% |
| 76% |
| 81% |
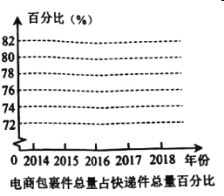
（1）直接写出
，
的值，并在图中画出电商包裹件总量占快递件总量百分比的折线统计图；
（2）若2019年该网点快递件总量预计达到7万件，请根据图表信息，估计2019年电商包裹件总量约为多少万件？
