Question

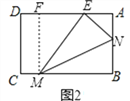
【题目】如图，在矩形中，点同时从点出发，分别在，上运动，若点的运动速度是每秒2个单位长度，且是点运动速度的2倍，当其中一个点到达终点时，停止一切运动．以为对称轴作的对称图形．点恰好在上的时间为__秒．在整个运动过程中，与矩形重叠部分面积的最大值为________________．

Answer 1

【答案】

【解析】分析：(1)如图,当B'与AD交于点E,作于F,根据轴对称的性质可以得出ME=MB=2t,由勾股定理就可以表示出EF,就可以表示出AE,再由勾股定理就可以求出t的值;(2)根据三角形的面积公式,分情况讨论,当和时由求分段函数的方法就可以求出结论.

详解：(1)如图,当B'与AD交于点E,作FM⊥AD于F,
∴∠DFM=90°.
∵四边形ABCD是矩形,
∴CD=AB ,AD=BC , ∠D=∠C=90°.
∴四边形DCMF是矩形,
∴CD=MF.
∵△MNB与△MNE关于MN对称,
∴△MNB≌△MNE,
∴ME=MB,NE=BN,.
∵BN=t,BM=2t,
∴EN=t,ME=2T.
∵AB=6,BC=8,
∴CD=MF=6,CB=DA=8,AN=6-t
在和中,由勾股定理,得
,,
,
,
.
,.
故答案为:;
(2)与关于MN对称,

.
,
.
,
.
,
.
∵四边形ABCD是矩形,
,
.
,,
,.
,,
,
,,
,
.
∴当时,
,
时,.
当时,.
时,.
.
∴最大值为.