题目内容
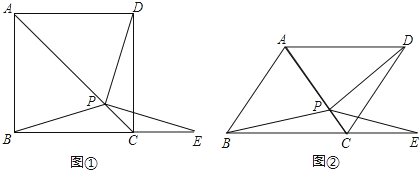
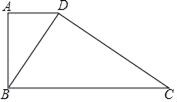
【题目】已知四边形ABCD中，∠BAD=∠BDC=90°，BD2=ADBC．
（1）求证：AD∥BC；
（2）过点A作AE∥CD交BC于点E．请完善图形并求证：CD2=BEBC．
【答案】（1）见解析；（2）见解析.
【解析】分析：（1）根据三角形的相似和平行线的性质可以证明结论成立；
（2）根据三角形的相似，对应边的比相等即可证明结论成立．
详解：（1）∵∠BAD=∠BDC=90°，BD2=ADBC，
∴
，∴△ADB∽△DBC，
∴∠ADB=∠DBC，∴AD∥BC；
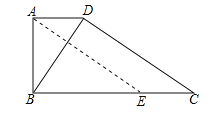
（2）如右图所示．
∵AD∥BC，AE∥DC，
∴四边形ADEC是平行四边形，∠AEB=∠BCD，∴AE=DC．
又∵∠BAD=∠BDC=90°，AD∥BC，
∴∠BAD+∠ABE=180°，∴∠ABE=90°，∴∠ABE=∠BDC，
∴△ABE∽△BDC，∴
，∴AEDC=BEBC．
∵AE=DC，∴CD2=BEBC．
练习册系列答案
相关题目
