题目内容
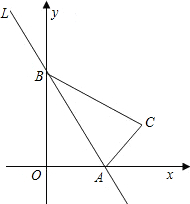 如图,直线1:y=-
如图,直线1:y=-| 3 |
| 3 |
分析:过点C作CE⊥x轴于点E,先根据直角三角形的性质求出OA,OB的长度,根据直角三角形特殊角的三角函数值可求得有关角的度数.利用轴对称性和直角三角函数值可求得AE,CE的长度,从而求得点A的坐标.
解答: 解:过点C作CE⊥x轴于点E
解:过点C作CE⊥x轴于点E
由直线AB的解析式可知
当x=0时,y=
,即OB=
当y=0时,x=1,即OA=1
∵∠AOB=∠C=90°,tan∠3=OB:OA=
∴∠3=60°
∵△AOB与△ACB关于直线l对称
∴∠2=∠3=60°,AC=OA=1
∴∠1=180°-∠2-∠3=60°
在RT△ACE中
AE=cos60°×AC=
×1=
CE=sin60°×AC=
∴OE=1+
=
∴点C的坐标是(
,
).
 解:过点C作CE⊥x轴于点E
解:过点C作CE⊥x轴于点E由直线AB的解析式可知
当x=0时,y=
| 3 |
| 3 |
当y=0时,x=1,即OA=1
∵∠AOB=∠C=90°,tan∠3=OB:OA=
| 3 |
∴∠3=60°
∵△AOB与△ACB关于直线l对称
∴∠2=∠3=60°,AC=OA=1
∴∠1=180°-∠2-∠3=60°
在RT△ACE中
AE=cos60°×AC=
| 1 |
| 2 |
| 1 |
| 2 |
CE=sin60°×AC=
| ||
| 2 |
∴OE=1+
| 1 |
| 2 |
| 3 |
| 2 |
∴点C的坐标是(
| 3 |
| 2 |
| ||
| 2 |
点评:本题主要考查了一次函数与直角三角形的综合运用和有关轴对称的性质.要熟练掌握根据函数解析式求得有关线段的长度的方法,灵活的运用数形结合的知识解题.

练习册系列答案
相关题目

 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( ) 4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )
4、如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( ) 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数 17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).
17、如图,直线a∥c,b∥c,直线d与直线a、b、c相交,已知∠1=60°,求∠2、∠3的度数(可在图中用数字表示角).