Question

如图，直线y=6-x交x轴、y轴于A、B两点，P是反比例函数y=

4

x

(x＞0)图象上位于直线下方的一点，过点P作x轴的垂线，垂足为点M，交AB于点E，过点P作y轴的垂线，垂足为点N，交AB于点F．则AF•BE=（　　）

• A、8
• B、6
• C、4
• D、6

  2

Answer 1

分析：首先作辅助线：过点E作EC⊥OB于C，过点F作FD⊥OA于D，然后由直线y=6-x交x轴、y轴于A、B两点，求得点A与B的坐标，则可得OA=OB，即可得△AOB，△BCE，△ADF是等腰直角三角形，则可得AF•BE=

2

CE•

2

DF=2CE•DF，又由四边形CEPN与MDFP是矩形，可得CE=PN，DF=PM，根据反比例函数的性质即可求得答案．

解答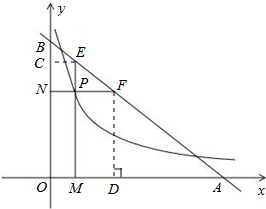：解：过点E作EC⊥OB于C，过点F作FD⊥OA于D，
∵直线y=6-x交x轴、y轴于A、B两点，
∴A（6，0），B（0，6），
∴OA=OB，
∴∠ABO=∠BAO=45°，
∴BC=CE，AD=DF，
∵PM⊥OA，PN⊥OB，
∴四边形CEPN与MDFP是矩形，
∴CE=PN，DF=PM，
∵P是反比例函数y=

4

x

(x＞0)图象上的一点，
∴PN•PM=4，
∴CE•DF=4，
在Rt△BCE中，BE=

CE

sin45°

=

2

CE，
在Rt△ADF中，AF=

DF

sin45°

=

2

DF，
∴AF•BE=

2

CE•

2

DF=2CE•DF=8．
故选A．

点评：此题考查了反比例函数的性质，以及矩形、等腰直角三角形的性质．解题的关键是注意数形结合与转化思想的应用．