题目内容
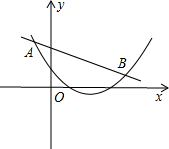
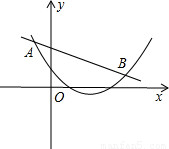
如图,直线:y1=kx+b与抛物线:y2=x2+bx+c交于点A(-2,4),B(8,2).
(1)求出直线解析式;
(2)求出使y1>y2的x的取值范围.
分析:(1)已知了直线图象上的两点坐标,即可由待定系数法求得该直线的解析式;
(2)观察图象,结合点A、B的坐标找出y1>y2时自变量的取值范围即可.
(2)观察图象,结合点A、B的坐标找出y1>y2时自变量的取值范围即可.
解答:解:(1)设直线AB的解析式为:y=kx+b,则有:
,
解得
;
故直线AB的解析式为:y=-
x+
.
(2)由两个函数的图象可知:当-2<x<8时,y1>y2.
|
解得
|
故直线AB的解析式为:y=-
| 1 |
| 5 |
| 18 |
| 5 |
(2)由两个函数的图象可知:当-2<x<8时,y1>y2.
点评:此题主要考查了用待定系数法求一次函数解析式的方法,以及通过两个函数的图象来判断不同自变量取值范围内函数值的变化情况,属于基础知识,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
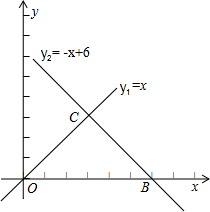 如图,直线OC,BC的函数关系式分别y1=x和y2=-x+6,动点P(x,0)在OB上运动(0<x<6),过点P作直线m与x轴垂直.
如图,直线OC,BC的函数关系式分别y1=x和y2=-x+6,动点P(x,0)在OB上运动(0<x<6),过点P作直线m与x轴垂直.