Question

【题目】如图，已知四边形是矩形，点在对角线上，点在边上（点与点、不重合），，且．

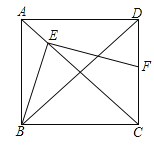
（1）求证：四边形是正方形；

（2）联结，交于点，求证：．

Answer 1

【答案】（1）四边形是正方形（过程见详解）

（2）（过程见详解）

【解析】

（1）本题借助辅助线利用，，找出∠DAC=45°得到DA=DC，即可证明，

（2）本题在（1）的条件下证明△CBE△DFQ，即可求证．

（1）

分别作EP⊥BC，EM⊥CD，

∵四边形ABCD为矩形，

∴∠ABE=∠BEP，

又BE⊥EF，

∴∠BEP+∠FEP=∠FEP+∠FEM=90°，

∴∠BEP =∠FEM，

∵，

∴，

∴，

即∠CEM=45°，

∴∠DAC=45°，

∴DA=DC，

∴矩形ABCD为正方形．

(2)

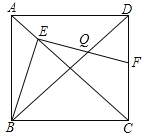
由(1)得：∠QDF=∠BCE=45°，，

∵，

∴，

∴，

即∠EBC=∠DFQ(三角形外角等于与其不相邻两内角和)，

∴△CBE△DFQ，

∴ ，

∴DFEC=DQBC，

即．