题目内容
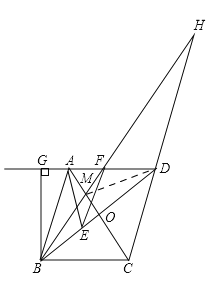
【题目】如图,在菱形ABCD中,AC与BD交于点O,E是BD上一点,EF//AB,∠EAB=∠EBA,过点B作DA的垂线,交DA的延长线于点G.
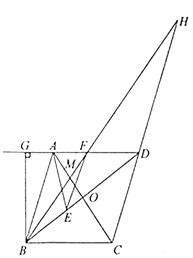
(1)∠DEF和∠AEF是否相等?若相等,请证明;若不相等,请说明理由;
(2)找出图中与ΔAGB相似的三角形,并证明;
(3)BF的延长线交CD的延长线于点H,交AC于点M.求证:BM2=MFMH.
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,证明见解析;(3)证明见解析.
,证明见解析;(3)证明见解析.
【解析】(1)先判断出∠DEF=∠EBA,∠AEF=∠EAB,即可得出结论;
(2)先判断出∠GAB=∠ABE+∠ADB=2∠ABE,进而得出∠GAB=∠AEO,即可得出结论;
(3)先判断出BM=DM,∠ADM=∠ABM,进而得出∠ADM=∠H,判断出△MFD∽△MDH,即可得出结论.
(1)∠DEF=∠AEF,理由如下:
∵EF∥AB,∴∠DEF=∠EBA,∠AEF=∠EAB.
∵∠EAB=∠EBA,∴∠DEF=∠AEF;
(2)△EOA∽△AGB,理由如下:
∵四边形ABCD是菱形,∴AB=AD,AC⊥BD,
∴∠GAB=∠ABE+∠ADB=2∠ABE.
∵∠AEO=∠ABE+∠BAE=2∠ABE.
∵∠GAB=∠AEO,∠GAB=∠AOE=90°,∴△EOA∽△AGB;
(3)如图,连接DM.
∵四边形ABCD是菱形,由对称性可知,BM=DM,∠ADM=∠ABM.
∵AB∥CH,∴∠ABM=∠H,∴∠ADM=∠H.
∵∠DMH=∠FMD,∴△MFD∽△MDH,∴![]() ,∴DM2=MFMH,
,∴DM2=MFMH,
∴BM2=MFMH.

【题目】为了加强市民的节水意识,合理利用水资源,某市采用阶梯收费的调控手段以达到节水的目的,该市自来水收费价目表如下:
每月用水量 | 价格 | 注:水费按月结算,每户每月须缴纳5元污水处理费. |
不超出6m3的部分 | 2元/m3 | |
超出6m3不超出10m3的部分 | 3元/m3 | |
超出10m3的部分 | 5元/m3 |
若某户居民![]() 月份用水
月份用水![]() ,则应缴费
,则应缴费![]() (元),
(元),
(1)若用户![]() 月份共用水
月份共用水![]() ,则需缴费________;
,则需缴费________;
(2)若该户居民某月缴费![]() 元,则该户居民该月用水多少吨?
元,则该户居民该月用水多少吨?