Question

【题目】如图，在正方形中，，分别是，上两个点，.

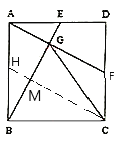
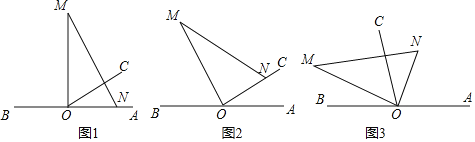
（1）如图1，与的关系是________；

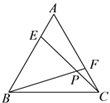
（2）如图2，当点是的中点时，（1）中的结论是否仍然成立，若成立，请进行证明；若不成立，说明理由；

（3）如图2，当点是的中点时，求证：.

Answer 1

【答案】（1）,;(2)成立，证明见解析；（3）见解析

【解析】

（1）因为，ABCD是正方形，所以AE=DF，可证△ADF≌BAE，可得=，再根据角∠AEB=∠AFD，∠DAF+∠AFD=90°，可得∠DAF+∠AEB=90°，可得;

（2）成立，因为E为AD中点，所以AE=DF，可证△ABE≌△DAF，可得=，再根据角∠AEB=∠AFD，∠DAF+∠AFD=90°，得到∠DAF+∠AEB=90°，可得；

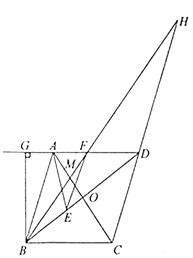
（3） 如解图，取AB中点H，连接CH交BG于点M，由（2）得，可证，所以MH为△AGB的中位线，所以M为BG中点，所以CM为BG垂直平分线，所以.

解：（1）AF=BE且AF⊥BE．理由如下：

证明：∵，ABCD为正方形

AE=AD－DE，DF=DC－CF

∴AE=DF

又∵∠BAD=∠D=90°，AB=AD

∴△ABE≌△DAF
∴AF=BE，∠AEB=∠AFD
∵在直角△ADF中，∠DAF+∠AFD=90°

∴∠DAF+∠AEB=90°

∴∠AGE=90°

∴AF⊥BE；

（2）成立，AF=BE且AF⊥BE．理由如下：

证明：∵E、F分别是AD、CD的中点，

∴AE=AD，DF=CD
∴AE=DF

又∵∠BAD=∠D=90°，AB=AD

∴△ABE≌△DAF
∴AF=BE，∠AEB=∠AFD
∵在直角△ADF中，∠DAF+∠AFD=90°

∴∠DAF+∠AEB=90°

∴∠AGE=90°

∴AF⊥BE

（3）取AB中点H，连接CH交BG于点M

∵H、F分别为AB、DC中点，AB∥CD，

∴AH=CF，

∴四边形AHCF是平行四边形，

∴AF∥CH，

又∵由（2）得，

∴，

∵AF∥CH，H为AB中点，

∴M为BG中点，

∵M为BG中点，且，

∴CH垂直平分BG，

∴CG=CB.